Протоколы Internet
IDEA - международный алгоритм шифрования данных
6.4.7 IDEA - международный алгоритм шифрования данных
Семенов Ю.А. (ГНЦ ИТЭФ)
IDEA является блочным алгоритмом шифрования данных, запатентованным швейцарской фирмой Ascom (http://fn2.freenet.edmonton.ab.ca/~jsavard/co0404.html). Фирма, правда, разрешила бесплатное некоммерческое использование своего алгоритма (применяется в общедоступном пакете конфиденциальной версии электронной почты PGP). Здесь в отличие от алгоритма DES не используются S-блоки или таблицы просмотра. В IDEA применяются 52 субключа, каждый длиной 16 бит. Исходный текст в IDEA делится на четыре группы по 16 бит. Для того чтобы комбинировать 16 битные коды, используется три операции: сложение, умножение и исключающее ИЛИ. Сложение представляет собой обычную операцию по модулю 65536 с переносом. При составлении таблицы умножения принимаются специальные меры для того, чтобы операция была обратимой. По этой причине вместо нуля используется код 65536. Рассмотрим алгоритм IDEA.
Пусть четыре четверти исходного текста имеют имена A, B, C и D, а 52 субключа – К(1), К(2),…, К(52). Перед реализацией алгоритма выполняются операции:
А = А*К(1); B = B + K(2); C = C + K(3); D = D * K(4);
Первый цикл вычислений включает в себя:
E = A XOR C; F = B XOR D
E = E * K(5)
F = F + E
F = F * K(6)
E = E + F
A = A XOR F
C = C XOR F
B = B XOR E
D = D XOR E
Меняем местами В и С.
Повторяем это всё 8 раз, используя К(7) – К(12) для второго раза и, соответственно, К(43) – К(48) - для восьмого. После восьмого раза В и С местами не меняются. Выполняем после этого операции:
A = A * K(49)
B = B + K(50)
C = C + K(51)
D = D * K(52)
В результате закодированный текст имеет ту же длину, что и исходный. Схема этого весьма запутанного алгоритма может быть пояснена на рис. 6.4.7.1. По своему характеру алгоритм напоминает процедуры вычисления хэш-функции.
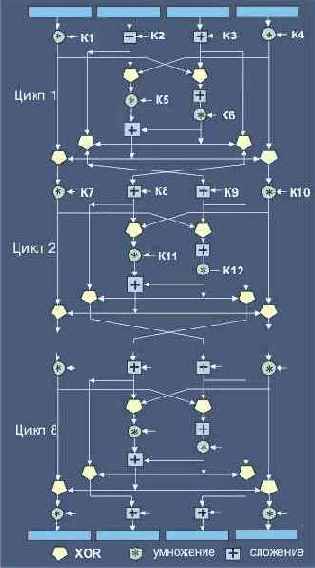
Рис. 6.4.7.1. Схема реализации алгоритма шифрования IDEA
При дешифровке используется тот факт, что A XOR B не изменяется, если C A и B будет произведена операция XOR C использованием любого числа. Это утверждение справедливо для любых значений А и В. Операции сложения (слагаемые заменяются их дополнением по модулю 2) и умножения (множители заменяются из обратными величинами по модулю 65537) также допускают инверсию. Первые четыре ключа дешифровки (KD) определяются несколько иначе, чем остальные.
KD(1) = 1/K(49);
KD(2) = -K(50);
KD(3) = -K(51);
KD(4) = 1/K(52);
Последующие операции производятся восемь раз с добавлением 6 к индексу ключей дешифрования и вычитанием 6 из индекса ключей шифрования.
KD(5) = K(47)
KD(6) = K(48)
KD(7) = 1/K(43)
KD(8) = -K(45)
KD(9) = -K(44)
KD(10) = 1/K(46)
Субключи IDEA генерируются следующим образом. 128-битовый ключ IDEA определяет первые восемь субключей (128=8*16). Последующие ключи (44) получаются путем последовательности циклических сдвигов влево этого кода на 25 двоичных разрядов.
SKIPJACK
Skipjack – секретный в прошлом блочный алгоритм, который ассоциируется с микросхемой Clipper (описание стало открытым в июне 1989 года). Алгоритм представляет собой альтернативу решениям, предлагаемым в алгоритмах IDEA и Safer (развитие идей DES, Lucifer и Blowfish). Блок исходных данных также как и в idea разбиваются на четыре группы. Алгоритм легко реализуется на обычной ЭВМ. Skipjack включает в себя 32 цикла шифрования. Эти циклы имеют две разновидности (А и В). Цикл А выполняет следующие операции.
Первая группа бит исходного текста подвергается шифрованию с использованием G-перестановок (четырех цикличный шифр Файстела – специальный класс блочных шифров, где зашифрованный текст получается из исходного путем многократного использования одного и того же преобразования, напоминает шифр DES. Исходный текст разделяется на две части. Функция преобразования f и ключ используются для преобразования одной из половин а результат объединяется со второй частью исходного кода с помощью операции исключающее ИЛИ. После этого части меняются местами и процедура повторяется и т.д.). Для полученного результата и номера цикла (RN = 1-32) и четвертой группы исходного текста (W4) выполняется операция XOR. После этого производится перенос: W1 -> W2; W2 -> W3; W3 -> W4; W4 -> W1.
Цикл В осуществляет следующие преобразования.
Для второй группы бит исходного текста (W2) выполняется операция XOR с номером цикла и первой группой бит исходного текста (W2 = (W2 XOR RN) XOR W1). Затем первая группа блока (W1) подвергается шифрованию с использованием G-перестановок. После этого производится перенос данных: W1 -> W2; W2 -> W3; W3 -> W4; W4 -> W1.
Последовательность выполнения алгоритма Skipjack предполагает выполнение 8 циклов типа А, 8 циклов В, 6 циклов А и 8 циклов В.
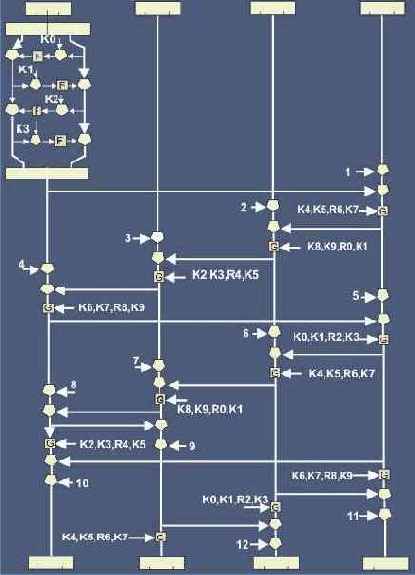
Рис. 6.4.7.2. Блок-схема алгоритма шифрования Skipjack
G-перестановки включают в себя разделение группы из 16 бит на две подгруппы по 8 бит. Подобно DES левая половина кода не изменяется в процессе реализации цикла шифрования, а используется в качестве входного параметра F-функции, для результата которой и правой части кода выполняется операция XOR. В отличии от DES половины кода меняются местами лишь после завершающего цикла.
F-функция G-перестановок достаточно проста: входные данные и субключ цикла объединяются операцией XOR, а результат заменяется кодом из таблицы просмотра (lookup-таблица - F). Субключи для G имеют длину 8 бит и являются первыми четырьмя байтами 80-битового исходного ключа. Первые 4 байта используются в первом цикле, следующие 4 – во втором, последние 2 байта вместе с первыми двумя – в третьем и т.д. 12 первых циклов реализации алгоритма шифрования Skipjack показаны на рис. 6.4.7.2. Первый цикл типа А отображен вместе со схемой реализации G-функции. Для следующих 7 циклов типа А G-функция отмечена квадратиком с буквой G. Цифрами (1-12) отмечен ввод данных для цикла с соответствующим номером. При реализации F-функции используется таблица (16*16) перестановок кодов 0-255.
В случае дешифровки циклы выполняются в обратном порядке. Аналогом цикла А при дешифровке является последовательность операций:
Для групп бит W1 и W2 и номера цикла выполняется операция XOR (циклы здесь нумеруются, начиная с 32 до 1). Затем W2 подвергается обратной G-перестановке, после чего выполняется перенос: W1 -> W4; W2 -> W1; W3 -> W2; W4 -> W3. Аналог цикла типа В при дешифровке включает в себя следующие операции:
Группа бит W2 подвергается обратной G-перестановке. W3 объединяется с номером цикла и группой бит W2 с помощью операции исключающее ИЛИ. После чего производится перемещение: W1 -> W4; W2 -> W1; W3 -> W2; W4 -> W3.
