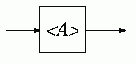
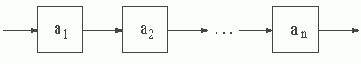Форма Наура-Бэкуса

При описании синтаксиса конкретных языков программирования приходится вводить большое число нетерминальных символов, и символическая форма записи теряет свою наглядность. В этом случае применяют форму Наура-Бэкуса (ФНБ), которая предполагает использование в качестве нетерминальных символов комбинаций слов естественного языка, заключенных в угловые скобки, а в качестве разделителя - специального знака, состоящего из двух двоеточий и равенства. Например, если правила <L>

® <L> и <L>

® <E> записаны в символической форме, и символ <L> соответствует синтаксическому понятию "список", а символ <E> - "элемент списка", то их можно представить в форме Наура-Бэкуса так: <список>::= <элемент списка><список>,
<список>::= <элемент списка>.

Чтобы сократить описание схемы грамматики, в ФБН разрешается объединять правила c одинаковой левой частью в одно правило, правая часть которого должна включать правые части объединяемых правил, разделенные вертикальной чертой. Используя объединение правил, для рассматриваемого примера получаем: <список>::=<элемент списка><список>|<элемент списка>.

Пред.Страница След.Страница Раздел Содержание

" Формальные языки, грамматики и автоматы"

Основными объектами изучения научного направления "Информатика" являются модели, представимые в памяти компьютера. Методы построения подобных моделей в различных предметных областях основаны на моделях конечных автоматов и формальных грамматик. Широкое использование таких моделей в теоретических исследованиях и разработке систем, используемых на практике, позволяет рассматривать их как одну из основ образования по направлению "Информатика". Главным назначением дисциплины "Формальные языки, грамматики и автоматы" является ознакомление студентов, обучающихся по направлению "Информатика" с основами теории, методами и приемами практического использования аппарата формальных грамматик и конечных автоматов. Изучение дисциплины планируется на 5-ом семестре и включает: курс лекций ( 4 часа в неделю ), лабораторные работы ( 2 часа в неделю ) и курсовую работу.
Лабораторные работы выполняются в компьютерном классе с использованием системы обучения синтаксическому анализу ( ОСА ). Эта система была разработана на кафедре Вычислительной техники в основном силами доц. Разумовского Г.В. и ассистента Кузнецова И.А. Она позволяет автоматизировать некоторые этапы синтеза магазинных автоматов и моделировать их работу.
В курсовой работе студенты реализуют программные модели магазинных преобразователей для некоторых фрагментов языков программирования.
В настоящее время ведется работа по созданию на базе курса лекций, и системы ОСА дистанционной обучающей системы, которая, в отличие от традиционных гипертекстовых представлений материала, должна обеспечивать интерактивное взаимодействие обучающегося с системой, автоматический контроль выполняемых заданий и возможность общения с преподавателем с помощью сетевых средств. Эта работа выполняется без финансовой поддержки в основном силами волонтеров - студентов. Считаю необходимым выразить благодарность моим помощницам Татьяне Карасевой и Светлане Новиковой, выполнившим преобразование текста в формат HTML.

Учитывая существующие трудности, публикацию электронной версии текста пособия предполагается выполнять частями в соответствии с планом пособия по мере их подготовки.

12.05.1998 В.Фомичев

Содержание курса

4. Описание перевода и преобразователи.

5. Атрибутные грамматики и преобразователи.

6. Автоматные грамматики и конечные автоматы.

7. Абстрактный синтез автоматов.

8. Переключательные функции и синтез комбинационных схем.

9. Структурный синтез автоматов.

4. Способы описания перевода. Бесскобочные выражения.

Преобразователи.

4.1. Описание перевода или трансляции .
4.1.1. Синтаксически - управляемые схемы
4.1.2. Перевод, определяемый СУ-схемой.
4.1.3. Простая СУ - схема.
4.1.4. Построение простой СУ - схемы.
4.1.5. Транслирующие грамматики
4.1.6. Входная и выходная грамматики заданной транслирующей грамматики.

4.1.7. Построение транслирующей грамматики по СУ - схеме
4.2. Бесскобочные выражения
4.2.1. Префиксная польская запись.
4.2.2. Вычисление префиксных польских записей.
4.2.3. Постфиксная польская запись.
4.2.4. Вычисление постфиксных польских записей.
4.2.5. Примеры постфиксных польских записей.
4.2.6. Примеры СУ - схем.
4.3. Магазинные Преобразователи.
4.3.1. Определение магазинного преобразователя.
4.3.2. Описание работы магазинного преобразователя.
4.3.3. Перевод определяемый преобразователем.
4.3.4. Построение преобразователя.
4.3.5. Пример построения детерминированного преобразователя.
4.3.6. Порядок построения детерминированного магазинного преобразователя.
4.4. Резюме.
4.5. Упражнения.
4.6. Термины.

Грамматика для описаний

Пусть требуется построить грамматику для описания целых и вещественных переменных. Описание переменных определенного типа должно начинаться указателем типа 'real' или 'int'.

В полном тексте описания описания переменных определенного типа могут повторяться. Например, полное описание может включать три разных описания переменных целого типа. Полное описание должно заканчиваться точкой. В качестве разделителя описаний переменных разных типов примем точку с запятой, а в качестве разделителя переменных одного типа - запятую. Структуру полного описания можно представить в виде двух вложенных списков с разделителями. Внутренний список, рассматриваемый как элемент внешнего списка, представляет собой описание переменных одного типа. Он имеет заголовок в виде указателя типа, за которым следует последовательность идентификаторов, разделенных запятыми. Внешний список использует в качестве разделителя точку с запятой. Схема грамматики рассматриваемого вида может быть записана так:

Г1. 26 : R = { <Z> ® <A2>,

<A2> ®

<B1><C1>,

<C1> ® ;<B1><C1>,

<C1> ® $,

<B1> ® 'real'<L>,

<B1> ® 'int'<L>,

<L> ® <K>,

<K> ® ,<K>,

<K> ® $ }

Пред.Страница След.Страница Раздел Содержание

Грамматика, задающая последовательность операторов присваивания

Допустим, что в правой части оператора присваивания могут быть использованы только выражения без скобок, описываемые грамматикой Г1. 24. В качестве разделителя операторов в последовательности примем точку с запятой. Учитывая, что последовательность операторов соответствует списку с разделителями в виде точки с запятой, и, используя определенную ранее конструкцию идентификатора, получаем искомую схему грамматики в виде:

Г1. 27 : R = { ® <A3>,

<A3> ® <S><R1>,

<R1> ® ;<S><R1>,

<R1> ® $,

<S> ® <B2>,

<B2> ® := <H1>,

<H1> ® <R2>,

<R2> ® +<R2>,

<R2> ® *<R2>,

<R2> ® $}

Пред.Страница След.Страница Раздел Содержание

Грамматики для арифметических выражений

Условимся рассматривать арифметические выражения, использующие только знаки сложения и умножения. Вначале построим грамматику для выражений без скобок. Такие выражения представляют собой цепочки, которые можно рассматривать как списки с разделителями, в которых роль разделителей выполняют знаки операций. В соответствии с этой аналогией получаем схему грамматики, в которой символ обозначает идентификатор, определение которого приведено выше.

Г1. 23 : R = { <H>

® <R>,

<R> ® <W><R>,

<R> ® $,

<W> ® +,

<W> ® * }.

Чтобы построить грамматику, допускающую использование в арифметических выражениях скобок без вложенности, представим структуру таких выражений в виде списка с разделителями, элементами которого являются выражения без скобок или выражения без скобок, заключенные в скобки. Разделителями этого списка являются знаки операций. Такой структуре соответствует следующая схема грамматики:

Г1. 24 : R = { <G>

® <H><Q>,

<G> ® (<H>)<Q>,

<Q> ® <W><G>,

<Q> ® $ }.

Для построения грамматики арифметических выражений, допускающих применение вложенных скобок, следует предусмотреть возможность использования в качестве элемента списка не только выражения без скобок, но и выражения, в котором могут быть использованы скобки. Схема грамматики, учитывающая эту возможность, может быть записана в виде:

Г1. 25 : R = { <E>

® <G>,

<E> ® (<E>),

® <W><E>,

® $ }.

Пред.Страница След.Страница Раздел Содержание

Грамматики, описывающие целые числа без знака и идентификаторы

Целые числа представляют собой последовательность цифр, поэтому их можно рассматривать как списки, элементами которых являются цифры. Используя в качестве аналога грамматику, задающую список без разделителей, получаем схему грамматики для целых чисел в виде:

Г1. 20: <N>

® <D><R>,

<R> ® <D><R>,

<R> ® $,

<D> ® 0 | 1 | ... | 9.

Структуру идентификатора можно представить в виде двух компонентов: начала и основной части. Началом может быть любая из букв, а основная часть представляет собой список без разделителей, элементами которого могут быть либо буквы, либо цифры. Используя выделенные компоненты, получаем схему грамматики вида:

Г1. 21: R ={ ® <C><A>,

<A> ® <C><A>|<D><A>,

<A> ® <C>|<D>,

<A> ® $,

<D> ® 0 | 1 | ... | 9,

<C> ® a | d | c | ... | z }.

Если наложить ограничения на длину идентификатора, например, допустить использование идентификаторов, состоящих только из трех символов, то схема грамматики получается проще.

Г1. 22 : R = { ® <C><A1>,

<A1> ® <C>,

<A1> ® <D>,

® <C>,

® <D>,

<D> ® 0 | 1 | ... | 9,

<C> ® a | d | c | ... | z }.

Пред.Страница След.Страница Раздел Содержание

Грамматики, описывающие условные операторы и операторы цикла

Допустим, что рассматриваются условные операторы, аналогичные используемым в языке Паскаль, с разделителями 'if', 'then', 'else'. В качестве условия в таких операторах разрешается использовать отношения, состоящие из двух идентификаторов, соединенных знаками = и <. Структура такого оператора определяется двумя видами последовательностей фиксированной длины, для описания которых можно воспользоваться простым перечислением компонентов. Первая последовательность определяет полный и сокращенный условные операторы, а вторая - конструкцию "отношение". Схема грамматики, задающая эти последовательности, может быть изображена так:

Г1. 28 : R = { <V>

® .if.<R4><C2>,

<C2> ® .then.<S><C3>,

<C3> ® .else.<S>,

<C3> ® $,

<R4> ® <R3>,

<R3> ® < ,

<R3> ® =

} .

В этой грамматике <S> определяется схемой грамматики Г1. 27 . Рассмотрим описание операторов цикла, подобных используемым в языке Паскаль, с разделителями 'while', 'do', 'repeat', 'until'. Каждый оператор может быть описан в виде простой последовательности ограниченной длины, в которой используются построенные ранее грамматика Г1. 28 и грамматика Г1. 27 . На практике часто встречаются ситуации, когда удобнее работать с грамматикой, правая часть правил которой начинается терминальным символом. Построение подобных грамматик сводится к тому, что для каждого терминального символа заданной конструкции языка строится отдельное правило. Для рассматриваемых операторов цикла такие схемы грамматик с использованием определенных ранее нетерминальных символов имеют вид:

Г1. 29: R = { <W> ® .while. <R4><C4>,

<C4> ® .do. <S> }

Г1. 30: R = { <W1>

® .repeat.<S><C5>,

<C5> ® .until.<R4>

Пред.Страница След.Страница Раздел Содержание

не имеют никаких ограничений на

Грамматики типа 0, которые называют грамматиками общего вида, не имеют никаких ограничений на правила порождения. Любое правило

r = h ® y

может быть построено с использованием произвольных цепочек

h, y О

(Vт И Va)*. Например,
<T><W> ® <W><T> или x<A>b<C><D> ® x<H><D>.

Пред.Страница След.Страница Раздел Содержание

не допускают использования любых правил.

Грамматики типа 1, которые называют также контекстно-зависимыми грамматиками, не допускают использования любых правил. Правила вывода в таких грамматиках должны иметь вид:

c1<A>c2 ® c1w c2,

где c1,

c2 - цепочки, возможно пустые, из множества

(Vт И Va)*,

символ <А> О Va

и цепочка w О (Vт И

Va)*. Цепочки c1

и c2 остаются неизменными при применении правила, поэтому их называют контекстом (соответственно левым и правым), а грамматику - контекстно зависимой.

Грамматики типа 1 значительно удобнее на практике, чем грамматики типа 0, поскольку в левой части правила заменяется всегда один нетерминальный символ, который можно связать с некоторым синтаксическим понятием, в то время как в грамматике типа 0 можно заменять сразу несколько символов, в том числе и терминальных.

Например, грамматика:

Г1. 4:

Vт = {a, b, c, d}, Va = {, <A>, }

R = { ® aA,

A ® AA,

AAA ® AA,

A ® b,

bA ® bcdA,

b ® ba }

является контекстно-зависимой, поскольку второе и шестое правила имеют непустой левый контекст, а третье и пятое правила содержат оба контекста. Вывод в такой грамматике может иметь вид:
 Ю a<A>

Ю a<A><A> Ю ab<A> Ю abb Ю abba.

Пред.Страница След.Страница Раздел Содержание

Правила вывода таких грамматик имеют

Грамматики типа 2

называют контектно-свободными и бесконтекстными грамматиками ( КС-грамматики или Б-грамматики).
Правила вывода таких грамматик имеют вид:

<A> ® a,

где <A> О

Va и a О (Vт И Va)*.
Очевидно, что эти правила получаются из правил грамматики типа 1 при условии c1

= c2 = $. Поскольку контекстные условия отсутствуют, то правила КС-грамматик получаются проще, чем правила грамматик типа 1. Именно такие грамматики используются для описания языков программирования. Примером КС-грамматики может служить следующая:

Г1. 5:

Vт = {a, b}, Va = {},

R = { ®

aa,

 ® bb,

 ® aa,

 ® bb}.

Эта грамматика порождает язык, который состоит из цепочек, каждая из которых в свою очередь состоит из двух частей, цепочки

b О Vт* и зеркального отображения этой цепочки b'.

L( Г5 ) = { bb' | b ОVт+},

где Vт+ - это множество Vт*

без пустой цепочки. С помощью правил этой грамматики может быть построена, например, следующая цепочка:
 Ю aa

Ю abba Ю abaaba

Ю ababbaba.

Пред.Страница След.Страница Раздел Содержание

в таких грамматиках имеют вид:

Грамматики типа 3

называют автоматными грамматиками (А - грамматиками). Правила вывода в таких грамматиках имеют вид:

<A> ® a

или <A> ® a

или <A> ® 

a,

где a О Vт, <A>, О Va, причем грамматика может иметь только правила вида <A>

® a - правосторонние правила, либо только вида <A> ® a

- левосторонние правила. Примерами автоматных грамматик могут служить правосторонняя грамматика Г1. 6

и левосторонняя грамматика Г1. 7.

Г1. 6:

Vт = {a, b}, Va = {, <A>},

R = { ® a,

 ® a<A>,

<A> ® b<A>,

<A> ® b<Z>,

<Z> ® $ }.

Г1. 7:

Vт = {a, b}, Va = {, <A>},

R = { ® <A>b,

<A> ® <A>b,

<A> ® <Z>a,

<Z> ® <Z>a,

<Z> ® $ }.

Эти грамматики являются эквивалентными и порождают язык

L(Г7) = {a...ab...b | n,m > 0}.

Между множествами языков различных типов существует отношение включения:

{ L типа 3 } М

{ L типа 2 }

М{ L типа 1 } М{ L типа 0}.

Доказано, что существуют языки типа 0, не являющиеся языками типа 1, языки типа 2, не являющиеся языками типа 1, и языки типа 3, не являющиея языками типа 2.

Учитывая, что наибольшее практическое применение находят грамматики типа 2 и типа 3, дальнейшее изложение посвящается рассмотрению именно этих типов грамматик.

Пред.Страница След.Страница Раздел Содержание

Итерационная форма

Для получения более компактных описаний синтаксиса применяют итерационную форму описания. Такая форма предполагает введение специальной операции, которая называется итерацией и обозначается парой фигурных скобок со звездочкой. Итерация вида {a}* определяется как множество, включающее цепочки всевозможной длины, построенные с использованием символа a, и пустую цепочку.

{a}* = {$, a, aa, aaa, aaaa,...}.

Иcпользуя итерацию для описания множества цепочек, задаваемых символическими правилами, для списка получаем:

<L> ® <E> {<E>}*.

Например, описание множества цепочек, каждая из которых должна начинаться знаком # и может состоять из произвольного числа букв x и y, может быть представлено в итерационной форме так:

® #{x | y}*

В итерационных формах описания наряду с итерационными cкобками часто применяют квадратные скобки для указания того, что цепочка , заключенная в них, может быть опущена. С помощью таких скобок правила:

® xz

могут быть записаны так:

<A> ® x[<A>y]z.

Пред.Страница След.Страница Раздел Содержание

<L>

, то получим правила грамматики в виде: Г1. 15: <L>

® a<R>,

<R> ® a<R>,

<R> ® $.

2) В предыдущей задаче предполагалось, что список <L>

должен содержать хотя бы один элемент. Если же допустить, что множество цепочек, порожденных правилами грамматики, может включать пустой символ, то к построенным правилам нужно добавить еще одно правило <L>

® $ . В этом случае набор правил имеет вид :

Г1. 16: <L> ® a<R>,

<R> ® a<R>,

<R> ® $,

<L> ® $.

3) Рассмотрим построение списка, между элементами которого должны стоять разделители. Выберем в качестве разделителя запятую. Простейший список, как и в предыдущем случае, состоит из одного элемента, а построение списка из нескольких элементов может быть выполнено приписыванием к уже построенной части списка разделителя с элементом списка. Правила, соответствующие этому построению, имеют вид:
Г1. 17: <L> ® a<R>,

<R> ® ,a<R>,

<R> ® $.

4) Если список с разделителями может быть пустым, то приведенный выше набор правил нужно дополнить еще одним правилом с пустой правой частью. В результате получим: Г1. 18: <L> ® a<R>,

<R> ® ,a<R>,

<R> ® $,

<L> ® $.

В общем случае, если описано множество цепочек, представляющих собой некоторый язык, и требуется построить грамматику, порождающую это множество цепочек, то следует поступать так:

1) Выписать несколько примеров из заданного множества цепочек.
2) Проанализировать структуру цепочек, выделяя начало, конец, повторяющиеся символы или группы символов.
3) Ввести обозначения для сложных структур, состоящих из групп символов. Такие обозначения являются нетерминальными символами искомой грамматики.
4) Построить правила для каждой из выделенных структур, используя для задания повторяющихся структур рекурсивные правила.
5) Объединить все правила.
6) Проверить с помощью выводов возможность получения цепочек с разной структурой.

Пред.Страница След.Страница Раздел Содержание

Левый и правый выводы

Среди всевозможных выводов наибольший интерес представляют следующие два типа выводов.

Определение. Если при построении вывода цепочки a

при каждом применении правила заменяется самый левый нетерминальный символ, то такой вывод называется левым или

левосторонним выводом a.

Если при построении вывода a, всегда заменяется самый правый нетерминальный символ промежуточной цепочки, то вывод называется правым или правосторонним

выводом a.

Например, приведенный выше вывод цепочки i * i + i в грамматике Г1. 9 является левосторонним выводом. Следует отметить, что различным выводам цепочки i+i в грамматике

Г1. 9 соответствует одно и то же синтаксическое дерево. Аналогичная ситуация имеет место и при выводе цепочки

i * i + i.

Пред.Страница След.Страница Раздел Содержание

Неоднозначные и эквивалентные грамматики

Существуют грамматики, в которых одна и та же цепочка может быть получена с помощью различных выводов. Например, в грамматике Г1. 10 цепочка abc

может быть получена с помощью двух различных выводов, и ей соответствуют два различных синтаксических дерева.

Г1. 10:

Vт = {a, b, c, d}, Va = {, <A>, },

R = { ® <A>,

<A> ® a,

<A> ® ac,

® b,

® cb}.

Первый вывод этой цепочки имеет вид :

1) Ю <A>

Ю <A>b Ю acb,

а второй можно получить так :

2) Ю <A>

Ю <A>cb Ю acb.

Этим выводам соответствуют разные синтаксические деревья и разборы :

Следующая грамматика также допускает построение одной и той же цепочки с помощью двух выводов, имеющих разные синтаксические деревья.

Г1. 11:

Vт = {0, +}, Va = {},

R = { ® 0,

®

+ 0,

® 0 +

Два вывода этой грамматики, порождающие одинаковые цепочки, имеют вид:

1) Ю

+ 0 Ю + 0 + 0 Ю 0 + 0 + 0,

2) Ю 0 + Ю 0 + 0 + Ю 0 + 0 + 0,

а синтаксические деревья, соответствующие этим выводам, можно изобразить так:

Рассмотренное свойство грамматик называется неоднозначностью. Оно может быть определено следующим образом.

Определение. Цепочка языка L(Г) называется неоднозначной, если для её вывода существует более чем одно синтаксическое дерево. Если грамматика Г порождает неоднозначную цепочку, то она называется неоднозначной.

Неоднозначность может существовать не только в искусственных языках. Хорошо известно, что в естественных языках могут быть предложения, допускающие неоднозначное написание. Например, "Пальто испачкало окно". В этой фразе не ясно, что является подлежащим, а что дополнением. Другим примером служит английская фраза: "They are flying planes", которая может быть понята двояко: "Они пилотируют самолет" или : Это летящие самолеты".

Свойство неоднозначности является крайне нежелательным для искусственных языков, поскольку оно не позволяет однозначным образом восстановить дерево вывода по заданной цепочке языка.
В общем случае можно сделать следующий вывод:
1) каждой цепочке, выводимой в грамматике, может соответствовать одно или несколько синтаксических деревьев,
2) каждому синтаксическому дереву могут соответствовать несколько выводов,
3) каждому синтаксическому дереву соответствует единственный правый и единственный левый выводы.
Кроме того, следует подчеркнуть, что один и тот же язык может быть получен с помощью различных грамматик.

Определение. Две грамматики Г1 и

Г2 называются эквивалентными, ecли они порождают один и тот же язык, т.е.

L(Г1) = L(Г2).

Пред.Страница След.Страница Раздел Содержание

Описание списков

В качестве первых примеров рассмотрим построение грамматик для последовательностей символов и последовательностей символов с разделителями. Такие последовательности часто называют списками.

1) Обозначим элемент последовательности a. Простейшая последовательность может состоять из одного элемента a. Все другие последовательности могут быть получены путем приписывания к уже построенной последовательности еще одного элемента. Если обозначить построенную часть последовательности нетерминальным символом <R>, а последовательность символом

Определение формальной грамматики и языка

Изучение предмета начнем с определения первичных понятий.

Первичные понятия

Определение. Конечное множество символов, неделимых в данном рассмотрении, называется словарем

или алфавитом, а символы, входящие в множество, - буквами алфавита.

Например, алфавит A = {a, b, c, +, !}

содержит 5 букв, а алфавит B = {00, 01, 10, 11}

содержит 4 буквы, каждая из которых состоит из двух символов.

Определение. Последовательность букв алфавита называется словом или цепочкой

в этом алфавите. Число букв, входящих в слово, называется его длиной.

Например, слово в алфавите A a=ab++c

имеет длину l(a) = 5, а слово в алфавите B b=00110010 имеет длину l (b) = 4.

Если задан алфавит A, то обозначим

A* множество всевозможных цепочек, которые могут быть построены из букв алфавита A. При этом предполагается, что пустая цепочка, которую обозначим знаком $, также входит в множество A*.

Определение. Формальной порождающей грамматикой

Построение грамматик и грамматики, описывающие основные конструкции языков программирования

Задача построения формальных грамматик состоит в том, что для заданного в виде описания на естественном языке множества конечных цепочек, требуется построить формальную грамматику, порождающую это множество цепочек. Учитывая, что терминальный словарь грамматики должен включать все символы, используемые для построения цепочек, входящих в заданное множество, результатом решения задачи должны явиться нетерминальный словарь и схема грамматики.
Построение этих объектов представляется весьма сложным, поскольку оно должно выполняться неформально и требует мысленного охвата всевозможных вариантов построения цепочек заданного множества и синтеза правил их построения. Построение усложняется еще и тем, что оно, как и всякая другая задача синтеза, имеет много решений.

Построение компилятора

Для построения компилятора необходимо однозначное и точное задание входного и выходного языков. Такое задание предполагает определение правил построения допустимых конструкций (выражений) языка. Множество таких правил называют синтаксисом

языка. Кроме того, задание должно включать описание назначения и смысла каждой конструкции языка. Такое описание называют семантикой

языка.

Для построения точных и недвусмысленных описаний применяют метод абстракций, который предполагает выделение наиболее существенных свойств рассматриваемого объекта и опускание свойств, менее значимых для рассматриваемого случая. Например, при построении модели входных языков можно рассматривать входной текст как последовательность символов, построенную по определенным правилам, отвлекаясь от характера начертания символов и их расположения на листе. Математические модели, использующие представление текстов в виде цепочек символов, называют формальными языками и грамматиками.

Пред.Страница След.Страница Раздел Содержание

Пример построения грамматик

Применение приведенных рекомендаций рассмотрим на следующем примере. Требуется построить грамматику для языка L ,терминальный словарь которого Vт = {*, |}, а цепочки, образующие язык, имеют следующую структуру: а) каждая цепочка начинается буквой * и заканчивается двумя буквами **.
b) между началом и концом цепочек могут быть: b1) либо непустая последовательность палочек
b2) либо несколько таких последовательностей, разделенных символами *.

1. Вначале построим несколько цепочек заданного языка, которые могут быть представлены в следующем виде:
* |**,
* |*|*|**,
* **|** ,
* |*|**** .

2. Рассматривая приведенные цепочки, можно выделить следующие их структурные компоненты:

начало цепочки (символ * ),

конец цепочки (символы ** ),

непустая группа палочек,

последовательность групп палочек, разделенных звездочками.

3. Обозначим группу палочек символом <A>, а последовательность групп палочек символом .
4. Выделенные структуры можно рассматривать как списки. Так последовательность палочек представляет собой список без разделителей, элементом которого является палочка. Правила грамматики, задающей такой список, имеют вид:

<A> ® | ,

 ® | ,

 ® $.

Последовательность групп палочек, разделенных звездочкой, представляет собой список с разделителем, элементом такого списка является группа палочек

<A>, а разделителем - звездочка. Правила грамматики, задающей такой список, можно записать так:

<C> ® <A><E>,

<E> ® *<A><E>,

<E> ® $.

Учитывая, что каждая цепочка языка должна иметь начало и конец, и , выбирая в качестве начального символа грамматики , получаем правило, определяющее общий вид цепочки:

 ® *<C>**.

5. Объединяя построенные правила, окончательно получаем схему искомой грамматики в виде:

Г1. 19: R = { ® *<C>**,

<C> ® <A><E>,

<E> ® *<A><E>,

<E> ® $,

<A> ® | ,

 ® | ,

 ® $ }
6. С помощью правил построенной грамматики может быть получена, например, следующая цепочка: Ю *<C>** Ю *<A><E>** Ю *<A>*<A><E>**
Ю
*<A>*<A>*<A><E> Ю *<A>*<A>*<A>**
Ю

*<A>*<A>* | ** Ю *<A>*<A>* | ** Ю

*<A>* | * | ** Ю *<A>* | * | ** Ю

* | * | * | ** Ю * | * | * | **.

Построенный вывод иллюстрирует возможность порождения цепочек заданного языка с помощью построенной грамматики.
Одной из основных областей применения формальных грамматик является описание языков программирования. Учитывая широкое использование подобных описаний в литературе и их важное значение для создания компиляторов, рассмотрим построение грамматик для основных конструкций языков программирования. Чтобы сократить размеры грамматик, на рассматриваемые конструкции накладываются некоторые, иногда существенные, ограничения.

Пред.Страница След.Страница Раздел Содержание

Примеры, иллюстрирующие первичные понятия

Рассмотрим несколько примеров, иллюстрирующих введенные понятия:

а) Задана грамматика Г1. 0 и требуется определить язык, порождаемый этой грамматикой: Г1. 0:

Vт = {a, b, c}, Va = {}, R = { ® abc}.

Схема грамматики содержит одно правило, поэтому Г1. 0 порождает язык из одного слова

L(Г1. 0) = {abc}.

b) Задана грамматика Г1. 1 и требуется определить язык, порождаемый этой грамматикой .

Г1. 1 :

Vт = {a, b, c}, Va = {, , <C>}

R = { ® a,

 ® <C>d,

 ® dc,

<C> ® $}.

Построим все выводы в этой грамматике:

 Ю

a Ю

a<C>d Ю

ad,

 Ю a

Ю adc.

Следовательно язык L(Г1. 1) = {adc, ad}.
в) Задана грамматика Г1. 2 и требуется определить язык, порождаемый этой грамматикой .

Г1. 2 : Va = {, <A>}, Vт = {0, 1},

R = { ® 0<A>1,

0<A> ® 00<A>1,

<A> ® $}.

Рассмотрим несколько выводов с помощью правил грамматики Г1. 2. Применяя первое и третье правила, получаем:

 Ю 0<A>1 Ю 01.

Применяя два раза первое правило и третье, имеем

 Ю 0<A>1 Ю 00<A>11 Ю 0011.

В общем случае, применяя K раз первое правило, получим в результате цепочку, содержащую K нулей и K единиц.
Следовательно, язык, порождаемый грамматикой

Г1. 2, содержит всевозможные цепочки, в которых число нулей равно числу единиц.
г) Задана грамматика Г1. 3 и требуется построить язык, порождаемый этой грамматикой.

Г1. 3 : Vт = {a, b}, Va = {, <A>},

R = { ® a<A>,

 <A> ® b<A>}.

Попытка построения вывода в этой грамматике приводит нас к цепочке: Ю a<A>

Ю ab<A> Ю abb<A>

Ю... ,

которая оказывается бесконечной. Другими словами, Г1. 3

порождает пустой язык.

Пред.Страница След.Страница Раздел Содержание

Пустой язык

Определение. Если язык, порождаемый грамматикой Г, не содержит ни одной конечной цепочки (конечного слова), то он называется пустым.

Утверждение. Для того, чтобы язык L( Г ) не был пустым, в множестве R

должно быть хотя бы одно правило вида r =

c ® y, где y О Vт* и должен существовать вывод

 Ю* c.

Пред.Страница След.Страница Раздел Содержание

Рекомендации по построению грамматик

Основой создания правил грамматики является способ выделения структуры заданного множества цепочек. Этот способ предусматривает расчленение цепочек, входящих в заданное множество, на части таким образом, чтобы выявить повторяющиеся части цепочек и части, входящие во все цепочки в неизменном виде. Такое расчленение на части представляет собой выявление структуры цепочек заданного множества.
Для каждого выявленного элемента структуры введем обозначения. Множество таких обозначений составляет основу словаря нетерминальных символов некоторой грамматики.
Следующим шагом построения является выявление последовательностей, в которых элементы структуры могут входить в заданные цепочки. Такие последовательности являются основой для построения правил грамматики.
Чтобы показать, каким образом структура цепочек отображается в правила грамматики, рассмотрим следующие примеры.
1. Цепочке, состоящей из заданных символов abc, соответствует правило

 ® abc.

2. Цепочке, начинающейся с заданного символа a, соответствует правило

 ® a<A>.

3. Цепочке, заканчивающейся заданным символом a, соответствует правило

 ® <A>a.

4. Цепочке, начинающейся и заканчивающейся заданными символами a, b, соответствует правило

 ® a<A>b.

5. Цепочке, содержащей в середине символ a, соответствует правило

 ® <A>a.

6. Цепочке заданной длины l =2 соответствуют правила:

<A> ® a

и ® a.

7. Цепочке, состоящей из повторяющихся символов a, соответствуют правила

<A> ® a<A>

и <A> ® a.

8. Цепочке, состоящей из чередующихся символов a и b, соответствуют правила:

<A> ® a

и ® b<A>.

Пред.Страница След.Страница Раздел Содержание

Для задания правил используются различные

Для задания правил используются различные формы описания: символическая, форма Наура-Бэкуса, итерационная форма и синтаксические диаграммы.
В практических применениях вместо символического представления схем грамматик обычно используют форму Наура-Бэкуса, или синтаксические диаграммы.

Задача построения формальной грамматики заключается в том, что по заданному описанию множества цепочек требуется определить словарь нетерминальных символов и построить схему грамматики. Эта задача относится к классу эвристических задач, не имеющих общих алгоритмов решения. На практике поиск решения выполняется с применением структурного анализа заданных цепочек. В результате такого анализа выявляются структурные компоненты цепочек, обозначения которых входят в нетерминальный словарь грамматики, а порядок следования компонентов в цепочках служит основой построения правил грамматики.

Пред.Страница След.Страница Раздел Содержание

Синтаксические диаграммы

Для того, чтобы улучшить зрительное восприятие и облегчить понимание сложных синтаксических описаний, применяют представление правил грамматики в виде синтаксических диаграмм. Правила построения таких диаграмм можно сформулировать в следующем виде:

1) Каждому правилу вида <A> ® a1

| a2 |...| ak ставится в соответствие диаграмма, структура которой определяется правой частью правила.
2) Каждое появление терминального символа x в цепочке ai

изображается на диаграмме дугой, помеченной этим символом x, заключенным в кружок.

3) Каждому появлению нетерминального символа <A> в цепочке ai ставится в соответствие на диаграмме дуга, помеченная символом, заключённым в квадрат.

4) Порождающее правило, имеющее вид:

<A> ® a1a2...an

изображается на диаграмме следующим образом:

5) Порождающее правило, имеющее вид:

<A> ® a1 | a2 | ... | an

изображается на диаграмме так:

6) Если порождающее правило задано в виде итерации:

<A> ® {a}*,

то ему соответствует диаграмма:

Число синтаксических диаграмм, которые можно построить для заданной схемы грамматики, определяется числом правил. Чтобы сократить число диаграмм, их объединяют, заменяя нетерминальные символы, входящие в диаграмму, построенными для них диаграммами.

Правила 3-6 предусматривают, что в качестве цепочки a1 на объединенной диаграмме могут быть использованы диаграммы построенные для этих цепочек. В качестве примера рассмотрим следующую грамматику с начальным символом <A> : Г1. 14: Vт = { x, +, (, ) }, Va = {<A>, , <C>},

R = {<A> ® x | (),

 ® <A><C>,

<C> ® {+<A>}*}.

Синтаксические диаграммы для такой грамматики имеют вид:

Заменяя нетерминальные символы, соответствующими диаграммами, получаем объединенную диаграмму в виде:

Пред.Страница След.Страница Раздел Содержание

Синтаксический разбор

Вывод цепочки с помощью правил грамматики может быть задан не только в виде синтаксического дерева. Если пронумеровать правила грамматики, то последовательность номеров используемых правил также задает вывод.

Определение. Последовательность номеров правил грамматики Г, применение которых позволяет построить вывод рассматриваемой цепочки s из начального символа грамматики, называется синтаксическим разбором s.

Например, в следующей грамматике

Г1. 9:

Vт = { i, +, * , (, ) }, Va = {<E>, <T>, }

R ={ (1) <E> ®<E>

+<T>,

(2) <E> ®<T>,

(3) <T> ®<T>

*,

(4) <T> ®,

(5) ®(E),

(6) ® i },

правила которой пронумерованы, вывод

<E> Ю <E>

+<T> Ю <T> +<T>

Ю <T> * +<T> Ю

 * +<T>

Ю i * +<T> Ю i * i +<T>

Ю

i * i + Ю

i * i + i

имеет синтаксический разбор [1,2,3,4,6,6,4,6].

Если в процессе построения вывода появляются промежуточные цепочки, содержащие несколько нетерминальных символов, то можно продолжать вывод, заменяя любой из них. Таким образом, одни и те же правила могут быть использованы при выводе цепочки в разном порядке.

Например, вывод цепочки i + i в грамматике Г1. 9 может быть получен десятью различными способами.

Пред.Страница След.Страница Раздел Содержание

Способы задания схем грамматик

Схема грамматики содержит правила вывода, определяющие синтаксис языка, или, другими словами, возможные компоненты и конструкции цепочек порождаемого языка. Для задания правил используются различные формы описания: символическая, форма Наура-Бэкуса, итерационная форма и синтаксические диаграммы.

В работах, связанных с рассмотрением общих свойств грамматик, обычно применяют символическую форму задания правил. Эта форма была рассмотрена в предыдущем параграфе. Она предусматривает использование в качестве элементов нетерминального словаря отдельных символов и стрелки в качестве разделителя правой и левой частей правила.

Стадии работы компилятора

Работа компилятора состоит из нескольких стадий, которые могут выполняться последовательно, либо совмещаться по времени. Эти стадии могут быть представлены в виде схемы.

Первая стадия работы компилятора называется лексическим анализом, а программа, её реализующая, - лексическим анализатором (ЛА). На вход лексического анализатора подаётся последовательность символов входного языка. ЛА выделяет в этой последовательности простейшие конструкции языка, которые называют лексическими единицами. Примерами лексических единиц являются идентификаторы, числа, символы операций, служебные слова и т.д. ЛА преобразует исходный текст, заменяя лексические единицы их внутренним представлением - лексемами. Лексема может включать информацию о классе лексической единицы и её значении. Кроме того, для некоторых классов лексических единиц ЛА строит таблицы, например, таблицу идентификаторов, констант, которые используются на последующих стадиях компиляции.

Вторую стадию работы компилятора называют синтаксическим анализом, а соответствующую программу - синтаксическим анализатором (СА). На вход СА подается последовательность лексем, которая преобразуется в промежуточный код,

представляющий собой последовательность символов действия или атомов. Каждый атом включает описание операции, которую нужно выполнить, с указанием используемых операндов. При этом последовательность расположения атомов, в отличие от лексем, соответствует порядку выполнения операций, необходимому для получения результата.

На третьей стадии работы компилятора осуществляется построение выходного текста. Программа, реализующая эту стадию, называется генератором выходного текста (Г). Генератор каждому символу действия, поступающему на его вход, ставит в соответствие одну или несколько команд выходного языка. В качестве выходного языка могут быть использованы команды устройства, команды ассемблера, либо операторы какого-либо другого языка.

Рассмотренная схема компилятора является упрощенной, поскольку реальные компиляторы, как правило, включают стадии оптимизации.

Пред.Страница След.Страница Раздел Содержание

Типы формальных языков и грамматик

В теории формальных языков выделяются 4 типа грамматик, которым соответствуют 4 типа языков. Эти грамматики выделяются путем наложения усиливающихся ограничений на правила грамматики.

Трансляторы , интерпретаторы и компиляторы

Транслятор может быть

интерпретирующего или компилирующего

типа. В первом случае его называют интерпретатором входного языка, а во втором - компилятором.

Интерпретатор последовательно читает предложения входного языка, анализирует их и сразу же выполняет, а компилятор не выполняет предложения языка, а строит программу, которая может в дальнейшем быть запущена для получения результата.

На вход компилятора подается текст, написанный на входном языке - языке, понятном человеку, а результатом работы компилятора является текст на языке, понятном устройству.

Пред.Страница След.Страница Раздел Содержание

Постройте синтаксическую диаграмму для грамматики

Постройте синтаксическую диаграмму для грамматики Г1. 5
.

1) Определите являются ли однозначными следующие грамматики:
Г1. 12:
Vт = {a}, Va = {, <A>},
R = { ® <A><A>,
<A> ® a,

<A> ® aa}.
Г1. 13:
Vт = {a, b, c}, Va = {, <A>, },
R = { ® a<A>c,
 ® $,

<A> ® c,

<A> ® <A>b,

 ® b,

 ® a}.
Пред.Страница След.Страница Раздел Содержание

1. Построить грамматики, порождающие следующие множества цепочек терминального словаря
Vт = {a, b}: а) множество всех слов, которые могут быть построены из символов словаря Vт*,
б) множество всех слов без пустой цепочки Vт+,
в) множество всех слов словаря Vт, начинающихся с буквы a.
г) множество L1 = {ab...b | n >= 0}
д) множество L2 = {b...ba | n >= 1}
2. Построить грамматики, порождающие следующие множества цепочек из символов терминального словаря Vт ={a, b, c}, в которых буква b может повторяться n раз. а) L3 = {ab...bc | n>=0}
б) L4 = {ab...bc | n>=1}
3. Построить грамматику, задающую язык, который состоит из цепочек, начинающихся символом $ и заканчивающихся символом ? , между которыми расположена непустая последовательность из знаков + и -, не содержащая двух одинаковых символов, стоящих рядом. Примеры цепочек: $+-?, $+?, $+-+-+?, $-+-+-?.
4. Построить грамматику, определяющую числа с порядком. Примеры: 3.2E-2, .5E+4, 162E3, -34E+20.
5. Построить грамматику для задания составных идентификаторов. Составной идентификатор может представлять собой несколько обычных идентификаторов, разделенных точкой. Примеры: PQ.F11 , SICN.X1.R , BL31.IN3.A6 .
6. Пусть задано множество биполярных сигналов потенциального типа, длительность которых изменяется дискретно. Начало и конец последовательности сигналов определяется сигналами отрицательной полярности.

Написать грамматику, задающую множество цепочек, соответствующих сигналам рассматриваемого типа, при условии, что состояния сигнала закодированы буквами a, b, c.
7. Построить грамматику, порождающую правильные выражения, состоящие из знаков &, V (конъюнкция, дизъюнкция), которые могут соединяться отношениями. Отношение строится из двух идентификаторов, соединенных знаками >, <, =,=/. Например, x>y V x>2 или x=a & x>b V x<c.
Пред.Страница След.Страница Раздел Содержание

изучающие вопросы появления разума на

Исследователи, изучающие вопросы появления разума на нашей планете, полагают, что решающую роль в его развитии сыграло появление языка, который позволил не только выражать и сохранять знания, но и обмениваться ими.
С созданием компьютеров, возникла потребность в общении с подобными устройствами, поскольку оказалось необходимым передавать им приказы, задания и описания работы, которую они должны выполнять. Для этой цели начали разрабатывать специальные языки, которые стали называть искусственными в отличие от естественных языков общения людей. Искусственные языки должны быть, с одной стороны, удобными и понятными для человека, а с другой - должны восприниматься устройствами. Совмещение этих требований в одном языке оказалось трудной задачей, поэтому появились средства для преобразования текстов с языка, понятного человеку, на язык устройства. Такие средства назвали трансляторами.

Вывод в КС-грамматиках и правила построения дерева вывода

Формальные грамматики позволяют задавать языки, представляющие множества цепочек, построенных по определенным правилам. Используемый способ задания позволяет построить любую цепочку, принадлежащую языку. Чтобы сделать процесс построения, называемый выводом, наглядным, его изображают в виде графа, точнее, в виде дерева, которое называют синтаксическим деревом или деревом вывода. Учитывая, что вывод любой цепочки языка, принадлежащей языку, порождаемому заданной грамматикой, должен начинаться с начального символа, правила построения дерева можно сформулировать так:

1) В качестве начальной вершины или корня дерева возьмем вершину, которую обозначим начальным символом грамматики ; эта вершина образует нулевой ярус дерева,

2) Если при выводе цепочки на очередном шаге используется правило грамматики <A> ® a

и вершина, помеченная нетерминалом <A>, расположена на ярусе с номером k-1, то к построенному дереву нужно добавить столько вершин, сколько содержится символов в цепочке a, расположить эти вершины на ярусе k , обозначить их символами цепочки a

и соединить эти вершины дугами с вершиной <A>.

Результатом вывода является множество конечных узлов - листьев, которые выписываются при обходе дерева слева - вниз - направо - вверх . Рассмотрим, например, грамматикy Г1. 8:

Г1. 8:

Vт = {a, b}, Va = {},

R = { ® ab,

® ab },

которая порождает язык L(Г8) = {aa...abb...b}, где а и b

повторяются по n раз,

n=1,2,...

Вывод цепочки с помощью правил этой грамматики имеет вид:

Пред.Страница След.Страница Раздел Содержание