Описание областей видимости и блочной структуры
Задачей контекстного анализа является установление свойств объектов и их использования. Наиболее часто решаемой задачей является определение существования объекта и соответствия его использования контексту, что осуществляется с помощью анализа типа объекта. Под контекстом здесь понимается вся совокупность свойств текущей точки программы, например множество доступных объектов, тип выражения и т.д.
Таким образом, необходимо хранить объекты и их типы, уметь находить эти объекты и определять их типы, определять характеристики контекста. Совокупность доступных в данной точке объектов будем называть средой. Обычно среда программы состоит из частично упорядоченного набора компонент
E = {DS1, DS2, ... , DSn}
Каждая компонента - это множество объявлений,

Рис. 6.1.
представляющих собой пары (имя, тип):
DSi = {(имяj, типj) | 1


где под типом будем подразумевать полное описание свойств объекта (объектом, в частности, может быть само описание типа).
Компоненты образуют дерево, соответствующее этому частичному порядку. Частичный порядок между компонентами обычно определяется статической вложенностью компонент в программе. Эта вложенность может соответствовать блокам, процедурам или классам программы (рис. 6.1). Компоненты среды могут быть именованы. Поиск в среде обычно ведется с учетом упорядоченности компонент. Среда может включать в себя как компоненты, полученные при трансляции "текущего" текста программы, так и "внешние" (например, раздельно компилированные) компоненты.
Для обозначения участков программы, в которых доступны те или иные описания, используются понятия области действия и области видимости. Областью действия описания является процедура (блок), содержащая описание, со всеми входящими в нее (подчиненными по дереву) процедурами (блоками). Областью видимости описания называется часть области действия, из которой исключены те подобласти, в которых по тем или иным причинам описание недоступно, например, оно перекрыто другим описанием. В разных языках понятия области действия и области видимости уточняются по-разному.
Обычными операциями при работе со средой являются:
включить объект в компоненту среды;найти объект в среде и получить доступ к его описанию;образовать в среде новую компоненту, определенным образом связанную с остальными;удалить компоненту из среды.
Среда состоит из отдельных объектов, реализуемых как записи (в дальнейшем описании мы будем использовать имя TElement для имени типа этой записи). Состав полей записи, вообще говоря, зависит от описываемого объекта (тип, переменная и т.д.), но есть поля, входящие в запись для любого объекта:
TObject Object - категория объекта (тип, переменная, процедура и т.д.);
TMode Mode - вид объекта: целый, массив, запись и т.д.;
TName Name - имя объекта;
TType Type - указатель на описание типа.
Занесение в среду и поиск объектов
Рассмотрим схему реализации простой блочной структуры, аналогичной процедурам в Паскале или блокам в Си. Каждый блок может иметь свой набор описаний. Программа состоит из основного именованного блока, в котором имеются описания и операторы. Описания состоят из описаний типов и объявлений переменных. В качестве типа может использоваться целочисленный тип и тип массива. Два типа T1 и T2 считаются эквивалентными, если имеется описание T1=T2 (или T2=T1). Операторами служат операторы присваивания вида Переменная1=Переменная2 и блоки. Переменная - это либо просто идентификатор, либо выборка из массива. Оператор присваивания считается правильным, если типы переменных левой и правой части эквивалентны.
Примером правильной программы может служить
program Example begin type T1=array 100 of array 200 of integer; T2=T1; var V1:T1; V2:T2; begin V1=V2; V2[1]=V1[2]; begin type T3=array 300 of T1; var V3:T3; V3[50]=V1; end end end.
Рассматриваемое подмножество языка может быть порождено следующей грамматикой (запись в расширенной БНФ):
Prog::='program' Ident Block '.' Block::='begin' [(Declaration)] [(Statement)] 'end' Declaration::='type' (Type_Decl) Type_Decl::=Ident '=' Type_Defin Type_Defin::='ARRAY' Index 'OF' Type_Defin Type_Defin::=Type_Use Type_Use::=Ident Declaration::='var' (Var_Decl) Var_Decl::=Ident_List ':' Type_Use ';' Ident_List::=(Ident / ',') Statement::=Block ';' Statement::=Variable '=' Variable ';' Variable::=Ident Access Access::='[' Expression ']' Access Access::=
Для реализации некоторых атрибутов (в частности среды, списка идентификаторов и т.д.) в качестве типов данных мы будем использовать различные множества. Множество может быть упорядоченным или неупорядоченным, ключевым или простым. Элементом ключевого множества может быть запись, одним из полей которой является ключ:
SETOF T - простое неупорядоченное множество объектов типа T; KEY K SETOF T - ключевое неупорядоченное множество объектов типа T с ключом типа K; LISTOF T - простое упорядоченное множество объектов типа T; KEY K LISTOF T - ключевое упорядоченное множество объектов типа T с ключом типа K;
Над объектами типа множества определены следующие операции:
Init(S) - создать и проинициализировать переменную S; Include(V,S) - включить объект V в множество S; если множество упорядоченное, то включение осуществляется в качестве последнего элемента; Find(K,S) - выдать указатель на объект с ключом K во множестве S и NIL, если объект с таким ключом не найден.
Имеется специальный оператор цикла, пробегающий элементы множества:
for (V in S) Оператор;
Переменная V пробегает все значения множества. Если множество упорядочено, то элементы пробегаются в этом порядке, если нет - в произвольном порядке.
Среда представляет собой ключевое множество с ключом - именем объекта. Идентификаторы имеют тип TName. Обозначение <Нетерминал> в позиции типа - это указатель на вершину типа Нетерминал. Обозначение <Нетерминал> в выражении - это взятие значения указателя
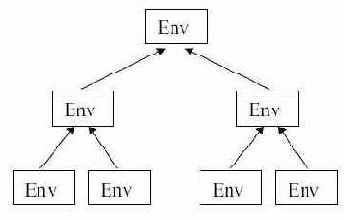
Рис. 6.2.
на ближайшую вершину вверх по дереву разбора, помеченную соответствующим нетерминалом.
Для реализации среды каждый нетерминал Block имеет атрибут Env. Для обеспечения возможности просматривать компоненты среды в соответствии с вложенностью блоков каждый нетерминал Block имеет атрибут Pred - указатель на охватывающий блок. Кроме того, среда блока корня дерева (нетерминал Prog) содержит все предопределенные описания (рис. 6.2). Это заполнение реализуется процедурой PreDefine. Атрибут Pred блока корневой компоненты имеет значение NULL.
Атрибутная реализация выглядит следующим образом.
Листинг 6.1.
(html, txt)
Переменная BlockPointer - указатель на ближайший охватывающий блок. Переходя от блока к блоку, ищем объект в его среде. Если не нашли, то переходим к охватывающему блоку. Если дошли до корневой компоненты, пытаемся найти объект среди предопределенных объектов. Если объект нашли, надо убедиться, что он имеет нужную категорию.
Функция ArrayElementType(TType EntryType, TType ExprType) осуществляет проверку допустимости применения операции взятия индекса к переменной и возвращает тип элемента массива.
Функция ArrayType(TType EntryType, int Val) возвращает описание типа - массива с типом элемента EntryType и диапазоном индекса Val.
Функции расстановки
Много внимания исследователями было уделено тому, какой должна быть (первичная) функция расстановки. Основные требования к ней очевидны: она должна легко вычисляться и распределять равномерно. Один из возможных подходов здесь заключается в следующем.
По символам строки s определяем положительное целое H. Преобразование одиночных символов в целые обычно можно сделать средствами языка реализации. В Паскале для этого служит функция ord, в Си при выполнении арифметических операций символьные значения трактуются как целые.Преобразуем H, вычисленное выше, в номер элемента, то есть целое между 0 и N - 1, где N - размер таблицы расстановки, например, взятием остатка при делении H на N. Функции расстановки, учитывающие все символы строки, распределяют лучше, чем функции, учитывающие только несколько символов, например, в конце или середине строки. Но такие функции требуют больше вычислений. Простейший способ вычисления H - сложение кодов символов. Перед сложением с очередным символом можно умножить старое значение H на константу q. То есть полагаем H0 = 0, Hi = q*Hi-1 + ci для 1


Переполнение при выполнении арифметических операций можно игнорировать. Функция Hashpjw, приведенная ниже [?], вычисляется, начиная с H = 0 (предполагается, что используются 32- битовые целые). Для каждого символа c сдвигаем биты H на 4 позиции влево и добавляем очередной символ. Если какой- нибудь из четырех старших бит H равен 1, сдвигаем эти 4 бита на 24 разряда вправо, затем складываем по модулю 2 с H и устанавливаем в 0 каждый из четырех старших бит, равных 1.
#define PRIME 211 #define EOS '\0' int Hashpjw(char *s) {char *p; unsigned H=0, g; for (p=s; *p!=EOS; p=p+1) {H=(H<<4)+(*p); if (g=H&0xf0000000) {H=H^(g>>24); H=H^g; } } return H%PRIME; }
Организация таблиц символов
В процессе работы компилятор хранит информацию об объектах программы в специальных таблицах символов. Как правило, информация о каждом объекте состоит из двух основных элементов: имени объекта и описания объекта. Информация об объектах программы должна быть организована таким образом, чтобы поиск ее был по возможности быстрее, а требуемая память по возможности меньше.
Кроме того, со стороны языка программирования могут быть дополнительные требования к организации информации. Имена могут иметь определенную область видимости. Например, поле записи должно быть уникально в пределах структуры (или уровня структуры), но может совпадать с именем объекта вне записи (или другого уровня записи). В то же время имя поля может открываться оператором присоединения, и тогда может возникнуть конфликт имен (или неоднозначность в трактовке имени). Если язык имеет блочную структуру, то необходимо обеспечить такой способ хранения информации, чтобы, во-первых, поддерживать блочный механизм видимости, а во-вторых - эффективно освобождать память при выходе из блока. В некоторых языках (например, Аде) одновременно (в одном блоке) могут быть видимы несколько объектов с одним именем, в других такая ситуация недопустима.
Мы рассмотрим некоторые основные способы организации таблиц символов в компиляторе: таблицы идентификаторов, таблицы расстановки, двоичные деревья и реализацию блочной структуры.
Реализация блочной структуры
С точки зрения структуры программы блоки (и/или процедуры) образуют дерево. Каждой вершине дерева этого представления, соответствующей блоку, можно сопоставить свою таблицу символов (и, возможно, одну общую таблицу идентификаторов). Работу с таблицами блоков можно организовать в магазинном режиме: при входе в блок создавать таблицу символов, при выходе - уничтожать. При этом сами таблицы должны быть связаны в упорядоченный список, чтобы можно было просматривать их в порядке вложенности. Если таблицы организованы с помощью функций расстановки, это означает, что для каждой таблицы должна быть создана своя таблица расстановки.
Сравнение методов реализации таблиц
Рассмотрим преимущества и недостатки рассмотренных методов реализации таблиц с точки зрения техники использования памяти.
Использование динамической памяти, как правило, довольно дорогая операция, поскольку механизмы поддержания работы с динамической памятью могут быть достаточно сложны. Необходимо поддерживать списки свободной и занятой памяти, выбирать наиболее подходящий кусок памяти при запросе, включать освободившийся кусок в список свободной памяти и, возможно, склеивать куски свободной памяти в списке.
С другой стороны, использование массива требует отведения заранее довольно большой памяти, а это означает, что значительная память вообще не будет использоваться. Кроме того, часто приходится заполнять не все элементы массива (например, в таблице идентификаторов или в тех случаях, когда в массиве фактически хранятся записи переменной длины, например, если в таблице символов записи для различных объектов имеют различный состав полей). Обращение к элементам массива может означать использование операции умножения при вычислении индексов, что может замедлить исполнение.
Наилучшим, по-видимому, является механизм доступа по указателям и использование факта магазинной организации памяти в компиляторе. Для этого процедура выделения памяти выдает необходимый кусок из подряд идущей памяти, а при выходе из процедуры вся память, связанная с этой процедурой, освобождается простой перестановкой указателя свободной памяти в состояние перед началом обработки процедуры. В чистом виде это не всегда, однако, возможно. Например, локальный модуль в Модуле-2 может экспортировать некоторые объекты наружу. При этом схему реализации приходится "подгонять" под механизм распределения памяти. В данном случае, например, необходимо экспортированные объекты вынести в среду охватывающего блока и свернуть блок локального модуля.
Таблицы идентификаторов
Как уже было сказано, информацию об объекте обычно можно разделить на две части: имя (идентификатор) и описание. Если длина идентификатора ограничена (или имя идентифицируется по ограниченному числу первых символов идентификатора), то таблица символов может быть организована в виде простого массива строк фиксированной длины, как это изображено на рис. 7.1. Некоторые входы могут быть заняты, некоторые - свободны.
Ясно, что, во-первых, размер массива должен быть не меньше числа идентификаторов, которые могут реально появиться в программе (в противном случае возникает переполнение таблицы); во-вторых, как правило, потенциальное число различных идентификаторов существенно больше размера таблицы.
Заметим, что в большинстве языков программирования символьное представление идентификатора может иметь произвольную длину. Кроме того, различные объекты в одной или в разных областях видимости могут иметь одинаковые имена, и нет большого смысла занимать память для повторного хранения идентификатора. Таким образом, удобно имя объекта и его описание хранить по отдельности. В этом случае идентификаторы хранятся в отдельной таблице - таблице идентификаторов. В таблице символов же хранится указатель на соответствующий вход в таблицу идентификаторов. Таблицу идентификаторов можно организовать, например, в виде сплошного массива. Идентификатор в массиве заканчивается каким-либо специальным символом EOS (рис. 7.2). Второй возможный

Рис. 7.1.

Рис. 7.2.
вариант - в качестве первого символа идентификатора в массив заносится его длина.
Таблицы на деревьях
Рассмотрим еще один способ организации таблиц символов с использованием двоичных деревьев.
Ориентированное дерево называется двоичным, если у него в каждую вершину, кроме одной (корня), входит одна дуга, и из каждой вершины выходит не более двух дуг. Ветвью дерева называется поддерево, состоящее из некоторой дуги данного дерева, ее начальной и конечной вершин, а также всех вершин и дуг, лежащих на всех путях, выходящих из конечной вершины этой дуги. Высотой дерева называется максимальная длина пути в этом дереве от корня до листа.
Пусть на множестве идентификаторов задан некоторый линейный (например, лексикографический) порядок




Рис. 7.5.
Каждой вершине двоичного дерева, представляющего таблицу символов, сопоставим идентификатор. При этом, если вершина (которой сопоставлен id) имеет левого потомка (которому сопоставлен idL), то


Поиск в такой таблице может быть описан следующей функцией:
struct TreeElement * SearchTree(String Id, struct TreeElement * TP) {int comp; if (TP==NULL) return NULL; comp=IdComp(Id,TP->IdentP); if (comp<0) return(SearchTree(Id,TP->Left)); if (comp>0) return(SearchTree(Id,TP->Right)); return TP; }
где структура для для элемента дерева имеет вид
struct TreeElement {String IdentP; struct TreeElement * Left, * Right; };
Занесение в таблицу осуществляется функцией
struct TreeElement * InsertTree(String Id, struct TreeElement * TP) {int comp=IdComp(Id,TP->IdentP); if (comp<0) return(Fill(Id,TP->Left, &(TP->Left))); if (comp>0) return(Fill(Id,TP->Right, &(TP->Right))); return(TP); }
struct TreeElement * Fill(String Id, struct TreeElement * P, struct TreeElement ** FP) { if (P==NULL) {P=alloc(sizeof(struct TreeElement)); P->IdentP=Include(Id); P->Left=NULL; P->Right=NULL; *FP=P; return(P); } else return(InsertTree(Id,P)); }
Как показано в работе [10], среднее время поиска в таблице размера n, организованной в виде двоичного дерева, при равной вероятности появления каждого объекта равно (2 ln 2) log2n + O(1). Однако, на практике случай равной вероятности появления объектов встречается довольно редко. Поэтому в дереве появляются более длинные и более короткие ветви, и среднее время поиска увеличивается.
Чтобы уменьшить среднее время поиска в двоичном дереве, можно в процессе построения дерева следить за тем, чтобы оно все время оставалось сбалансированным. А именно, назовем дерево сбалансированным, если ни для какой вершины высота выходящей из нее правой ветви не отличается от высоты левой более чем на 1. Для того, чтобы достичь сбалансированности, в процессе добавления новых вершин дерево можно слегка перестраивать следующим образом [1].
Определим для каждой вершины дерева характеристику, равную разности высот выходящих из нее правой и левой ветвей. В сбалансированном дереве характеристика вершины может быть равной -1, 0 и 1, для листьев она равна 0.
Пусть мы определили место новой вершины в дереве. Ее характеристика равна 0. Назовем путь, ведущий от корня к новой вершине, выделенным. При добавлении новой вершины могут измениться характеристики только тех вершин, которые лежат на выделенном пути. Рассмотрим заключительный отрезок выделенного пути, такой, что до добавления вершины характеристики всех вершин на нем были равны 0. Если верхним концом этого отрезка является сам корень, то дерево перестраивать не надо, достаточно лишь изменить характеристики вершин на этом пути на 1 или -1, в зависимости от того, влево или вправо пристроена новая вершина.

Рис. 7.6.

Рис. 7.7.
Пусть верхний конец заключительного отрезка - не корень. Рассмотрим вершину A - "родителя" верхнего конца заключительного отрезка. Перед добавлением новой вершины характеристика A была равна

Так что и в этом случае дерево перестраивать не надо. Пусть теперь характеристика A до перестраивания была равна -1 и новая вершина добавлена к левой ветви A (аналогично - для случая 1 и добавления к правой ветви). Рассмотрим вершину B - левого потомка A. Возможны следующие варианты.

Рис. 7.8.

Рис. 7.9.
Если характеристика B после добавления новой вершины в D стала равна -1, то дерево имеет структуру, изображенную на рис. 7.6, а. Перестроив дерево так, как это изображено на рис. 7.6, б, мы добьемся сбалансированности (в скобках указаны характеристики вершин, где это существенно, и соотношения высот после добавления).
Если характеристика вершины B после добавления новой вершины в E стала равна 1, то надо отдельно рассмотреть случаи, когда характеристика вершины E, следующей за B на выделенном пути, стала равна -1, 1 и 0 (в последнем случае вершина E - новая). Вид дерева до и после перестройки для этих случаев показан соответственно на рис. 7.7, рис. 7.8 и рис. 7.9.
Таблицы расстановки
Одним из эффективных способов организации таблицы символов является таблица расстановки (или хеш-таблица). Поиск в такой таблице может быть организован методом повторной расстановки. Суть его заключается в следующем.
Таблица символов представляет собой массив фиксированного размера N. Идентификаторы могут храниться как в самой таблице символов, так и в отдельной таблице идентификаторов.
Определим некоторую функцию h1 (первичную функцию расстановки), определенную на множестве идентификаторов и принимающую значения от 0 до N - 1 (то есть 0

h1(id)

Пусть мы хотим найти в таблице идентификатор id. Если элемент таблицы с номером h1(id) не заполнен, то это означает, что идентификатора в таблице нет. Если же занят, то это еще не означает, что идентификатор id в таблицу занесен, поскольку (вообще говоря) много идентификаторов могут иметь одно и то же значение функции расстановки. Для того чтобы определить, нашли ли мы нужный идентификатор, сравниваем id с элементом таблицы h1(id). Если они равны - идентификатор найден, если нет - надо продолжать поиск дальше.
Для этого вычисляется вторичная функция расстановки h2(h) (значением которой опять таки является некоторый адрес в таблице символов). Возможны четыре варианта:
элемент таблицы не заполнен (то есть идентификатора в таблице нет),идентификатор элемента таблицы совпадает с искомым (то есть идентификатор найден),адрес элемента совпадает с уже просмотренным (то есть таблица вся просмотрена и идентификатора нет)предыдущие варианты не выполняются, так что необходимо продолжать поиск.
Для продолжения поиска применяется следующая функция расстановки h3(h2), h4(h3) и т.д. Как правило, hi = h2 для i

h2(i) = (i + 1) mod N. Берется следующий (циклически) элемент массива.
Этот вариант плох тем, что занятые элементы "группируются" , образуют последовательные занятые участки и в пределах этого участка поиск становится по-существу линейным. h2(i) = (i + k) mod N, где k и N взаимно просты. По-существу это предыдущий вариант, но элементы накапливаются не в последовательных элементах, а "разносятся".h2(i) = (a * i + c) mod N - "псевдослучайная последовательность". Здесь c и N должны быть взаимно просты, b = a-1 кратно p для любого простого p, являщегося делителем N, b кратно 4, если N кратно 4 [6].
Поиск в таблице расстановки можно описать следующей функцией:
void Search(String Id,boolean * Yes,int * Point) {int H0=h1(Id), H=H0; while (1) {if (Empty(H)==NULL) {*Yes=false; *Point=H; return; } else if (IdComp(H,Id)==0) {*Yes=true; *Point=H; return; } else H=h2(H); if (H==H0) {*Yes=false; *Point=NULL; return; } } }
Функция IdComp(H,Id) сравнивает элемент таблицы на входе H с идентификатором и вырабатывает 0, если они равны. Функция Empty(H) вырабатывает NULL, если вход H пуст. Функция Search присваивает параметрам Yes и Pointer соответственно следующие значения :
true, P - если нашли требуемый идентификатор, где P - указатель на соответствующий этому идентификатору вход в таблице,
false, NULL - если искомый идентификатор не найден, причем в таблице нет свободного места, и
false, P - если искомый идентификатор не найден, но в таблице есть свободный вход P.
Занесение элемента в таблицу можно осуществить следующей функцией:
int Insert(String Id) {boolean Yes; int Point=-1; Search(Id,&Yes,&Point); if (!Yes && (Point!=NULL)) InsertId(Point,Id); return(Point); }
Здесь функция InsertId(Point,Id) заносит идентификатор Id для входа Point таблицы.
Таблицы расстановки со списками
Только что описанная схема страдает одним недостатком - возможностью переполнения таблицы. Рассмотрим ее модификацию, когда все элементы, имеющие одинаковое значения (первичной) функции расстановки, связываются в список (при этом отпадает необходимость использования функций hiдля i

Вначале таблица расстановки пуста (все элементы имеют значение NULL). При поиске идентификатора Id вычисляется функция расстановки h(Id) и просматривается соответствующий линейный список. Поиск в таблице может быть описан следующей функцией:
struct Element {String IdentP; struct Element * Next; }; struct Element * T[N];
struct Element * Search(String Id) {struct Element * P; P=T[h(Id)]; while (1) {if (P==NULL) return(NULL); else if (IdComp(P->IdentP,Id)==0) return(P); else P=P->Next; } }
Занесение элемента в таблицу можно осуществить следующей функцией:
struct Element * Insert(String Id) {struct Element * P,H; P=Search(Id); if (P!=NULL) return(P); else {H=H(Id); P=alloc(sizeof(struct Element)); P->Next=T[H]; T[H]=P; P->IdentP=Include(Id); } return(P); }
Процедура Include заносит идентификатор в таблицу идентификаторов. Алгоритм иллюстрируется рис. 7.4.

Рис. 7.3.

Рис. 7.4.
Линеаризованные представления
В качестве промежуточных представлений весьма распространены линеаризованные представления деревьев. Линеаризованное представление позволяет относительно легко хранить промежуточное представление во внешней памяти и обрабатывать его. Наиболее распространенной формой линеаризованного представления является польская запись - префиксная (прямая) или постфиксная (обратная).
Постфиксная запись - это список вершин дерева, в котором каждая вершина следует (при обходе снизу-вверх слева-направо) непосредственно за своими потомками. Дерево на рис. 8.1, а, в постфиксной записи может быть представлено следующим образом:
a b c - * b c - * + :=
В постфиксной записи вершины синтаксического дерева явно не присутствуют. Они могут быть восстановлены из порядка, в котором следуют вершины и из числа операндов соответствующих операций. Восстановление вершин аналогично вычислению выражения в постфиксной записи с использованием стека.
В префиксной записи сначала указывается операция, а затем ее операнды. Например, для приведенного выше выражения имеем
:= a + * b - c * b - c
Рассмотрим детальнее одну из реализаций префиксного представления - Лидер [12]. Лидер - это аббревиатура от "ЛИнеаризованное ДЕРево". Это машинно-независимая префиксная запись. В Лидере сохраняются все объявления и каждому из них присваивается свой уникальный номер, который используется для ссылки на объявление. Рассмотрим пример.
module M; var X,Y,Z: integer; procedure DIF(A,B:integer):integer; var R:integer; begin R:=A-B; return(R); end DIF; begin Z:=DIF(X,Y); end M.
Этот фрагмент имеет следующий образ в Лидере.
program 'M' var int var int var int procbody proc int int end int var int begin assign var 1 7 end int int mi par 1 5 end par 1 6 end result 0 int var 1 7 end return end begin assign var 0 3 end int icall 0 4 int var 0 1 end int var 0 2 end end end
Рассмотрим его более детально:
| program 'M' | Имя модуля нужно для редактора связей. |
| var int | Это образ переменных X, Y, Z; |
| var int | переменным X, Y, Z присваиваются |
| var int | номера 1, 2, 3 на уровне 0. |
| procbody proc | Объявление процедуры с двумя |
| int int end | целыми параметрами, возвращающей целое. |
| int | Процедура получает номер 4 на уровне 0 и параметры имеют номера 5, 6 на уровне 1. |
| var int | Переменная R имеет номер 7 на уровне 1. |
| begin | Начало тела процедуры. |
| assign | Оператор присваивания. |
| var 1 7 end | Левая часть присваивания (R). |
| int | Тип присваиваемого значения. |
| int mi | Целое вычитание. |
| par 1 5 end | Уменьшаемое (A) |
| par 1 6 end | Вычитаемое (B) |
| result 0 | Результат процедуры уровня 0 |
| int | Результат имеет целый тип |
| var 1 7 end | Результат - переменная R |
| return | Оператор возврата |
| end | Конец тела процедуры |
| begin | Начало тела модуля. |
| assign | Оператор присваивания. |
| var 0 3 end | Левая часть - переменная Z. |
| int | Тип присваиваемого значения. |
| icall 0 4 | Вызов локальной процедуры DIF |
| int var 0 1 end | Фактические параметры X |
| int var 0 2 end | и Y |
| end | Конец вызова. |
| end | Конец тела модуля |
Набор команд виртуальной машины
Виртуальная Java-машина имеет следующие команды:
| помещение констант на стек, |
| помещение локальных переменных на стек, |
| запоминание значений из стека в локальных переменных, |
| обработка массивов, |
| управление стеком, |
| арифметические команды, |
| логические команды, |
| преобразования типов, |
| передача управления, |
| возврат из функции, |
| табличный переход, |
| обработка полей объектов, |
| вызов метода, |
| обработка исключительных ситуаций, |
| прочие операции над объектами, |
| мониторы, |
| отладка. |
Рассмотрим некоторые команды подробнее.
Организация информации в генераторе кода
Синтаксическое дерево в чистом виде несет только информацию о структуре программы. На самом деле в процессе генерации кода требуется также информация о переменных (например, их адреса), процедурах (также адреса, уровни), метках и т.д. Для представления этой информации возможны различные решения. Наиболее распространены два:
информация хранится в таблицах генератора кода;информация хранится в соответствующих вершинах дерева.
Рассмотрим, например, структуру таблиц, которые могут быть использованы в сочетании с Лидер-представлением. Поскольку Лидер-представление не содержит информации об адресах переменных, значит, эту информацию нужно формировать в процессе обработки объявлений и хранить в таблицах. Это касается и описаний массивов, записей и т.д. Кроме того, в таблицах также должна содержаться информация о процедурах (адреса, уровни, модули, в которых процедуры описаны, и т.д.).
При входе в процедуру в таблице уровней процедур заводится новый вход - указатель на таблицу описаний. При выходе указатель восстанавливается на старое значение. Если промежуточное представление - дерево, то информация может храниться в вершинах самого дерева.
Организация памяти
Машина имеет следующие регистры: pc - счетчик команд; optop - указатель вершины стека операций; frame - указатель на стек-фрейм исполняемого метода; vars - указатель на 0-ю переменную исполняемого метода. Все регистры 32-разрядные. Стек-фрейм имеет три компоненты: локальные переменные, среду исполнения, стек операндов. Локальные переменные отсчитываются от адреса в регистре vars. Среда исполнения служит для поддержания самого стека. Она включает указатель на предыдущий фрейм, указатель на собственные локальные переменные, на базу стека операций и на верхушку стека. Кроме того, здесь же хранится некоторая дополнительная информация, например, для отладчика.
Куча сборки мусора содержит экземпляры объектов, которые создаются и уничтожаются автоматически. Область методов содержит коды, таблицы символов и т.д. С каждым классом связана область констант. Она содержит имена полей, методов и другую подобную информацию, которая используется методами.
Представление в виде ориентированного графа
Простейшей формой промежуточного представления является синтаксическое дерево программы. Ту же самую информацию о входной программе, но в более компактной форме дает ориентированный ациклический граф (ОАГ), в котором в одну вершину объединены вершины синтаксического дерева, представляющие общие подвыражения. Синтаксическое дерево и ОАГ для оператора присваивания
a := b *-c + b * -c
приведены на рис. 8.1

Рис. 8.1.

Рис. 8.2.
На рис. 8.2 приведены два представления в памяти синтаксического дерева на рис. 8.1, а. Каждая вершина кодируется записью с полем для операции и полями для указателей на потомков. На рис. 8.2, б, вершины размещены в массиве записей и индекс (или вход) вершины служит указателем на нее.
Промежуточное представление программы
В процессе трансляции компилятор часто используют промежуточное представление (ПП) исходной программы, предназначенное прежде всего для удобства генерации кода и/или проведения различных оптимизаций. Сама форма ПП зависит от целей его использования.
Наиболее часто используемыми формами ПП является ориентированный граф (в частности, абстрактное синтаксическое дерево, в том числе атрибутированное), трехадресный код (в виде троек или четверок), префиксная и постфиксная запись.
Трехадресный код
Трехадресный код - это последовательность операторов вида x := y op z, где x, y и z - имена, константы или сгенерированные компилятором временные объекты. Здесь op - двуместная операция, например операция плавающей или фиксированной арифметики, логическая или побитовая. В правую часть может входить только один знак операции.
Составные выражения должны быть разбиты на подвыражения, при этом могут появиться временные имена (переменные). Смысл термина "трехадресный код" в том, что каждый оператор обычно имеет три адреса: два для операндов и один для результата. Трехадресный код - это линеаризованное представление синтаксического дерева или ОАГ, в котором временные имена соответствуют внутренним вершинам дерева или графа. Например, выражение x + y * z может быть протранслировано в последовательность операторов
t1 := y * z t2 := x + t1
где t1 и t2 - имена, сгенерированные компилятором. В виде трехадресного кода представляются не только двуместные операции, входящие в выражения. В таком же виде представляются операторы управления программы и одноместные операции. В этом случае некоторые из компонент трехадресного кода могут не использоваться. Например, условный оператор
if A > B then S1 else S2
может быть представлен следующим кодом:
t := A - B JGT t, S2 ...
Здесь JGT - двуместная операция условного перехода, не вырабатывающая результата.
Разбиение арифметических выражений и операторов управления делает трехадресный код удобным при генерации машинного кода и оптимизации. Использование имен промежуточных значений, вычисляемых в программе, позволяет легко переупорядочивать трехадресный код.
| а | б |
| t1 := -c | t1 := -c |
| t2 := b * t1 | t2 := b * t1 |
| t3 := -c | t5 := t2 + t2 |
| t4 := b * t3 | a := t5 |
| t5 := t2 + t4 | |
| a := t5 |
Представления синтаксического дерева и графа рис. 8.1
в виде трехадресного кода дано в таблица 8.1, а, и таблица 8.1, б, соответственно.
Трехадресный код - это абстрактная форма промежуточного кода. В реализации трехадресный код может быть представлен записями с полями для операции и операндов.
Рассмотрим три способа реализации трехадресного кода: четверки, тройки и косвенные тройки.
Четверка - это запись с четырьмя полями, которые будем называть op, arg1, arg2 и result. Поле op содержит код операции. В операторах с унарными операциями типа x := -y или x := y поле arg2 не используется. В некоторых операциях (типа "передать параметр") могут не использоваться ни arg2, ни result. Условные и безусловные переходы помещают в result метку перехода. На рис. 8.2, а, приведены четверки для оператора присваивания a := b *-c+b *-c. Они получены из трехадресного кода в таблица 8.1, а.
| op | arg1 | arg2 | result | |
| (0) | - | c | t1 | |
| (1) | * | b | t1 | t2 |
| (2) | - | c | t3 | |
| (3) | * | b | t3 | t4 |
| (4) | + | t2 | t4 | t5 |
| (5) | := | t5 | a |
| op | arg1 | arg2 | |
| (0) | - | c | |
| (1) | * | b | (0) |
| (2) | - | c | |
| (3) | * | b | (2) |
| (4) | + | (1) | (3) |
| (5) | := | a | (4) |
Обычно содержимое полей arg1, arg2 и result - это указатели на входы таблицы символов для имен, представляемых этими полями. Временные имена вносятся в таблицу символов по мере их генерации.
Чтобы избежать внесения новых имен в таблицу символов, на временное значение можно ссылаться, используя позицию вычисляющего его оператора. В этом случае трехадресные операторы могут быть представлены записями только с тремя полями: op, arg1 и arg2, как это показано в таблица 8.2б Поля arg1 и arg2 - это либо указатели на таблицу символов (для имен, определенных программистом, или констант), либо указатели на тройки (для временных значений). Такой способ представления трехадресного кода называют тройками. Тройки соответствуют представлению синтаксического дерева или ОАГ с помощью массива вершин.
Числа в скобках - это указатели на тройки, а имена - это указатели на таблицу символов. На практике информация, необходимая для интерпретации различного типа входов в поля arg1 и arg2, кодируется в поле op или дополнительных полях. Тройки таблица 8.2б, соответствуют четверкам таблица 8.2a
Для представления тройками трехместной операции типа x[i] := y требуется два входа, как это показано в таблица 8.3а, представление x := y[i] двумя операциями показано в таблица 8.3б
| op | arg1 | arg2 | |
| (0) | []= | x | i |
| (1) | := | (0) | y |
| op | arg1 | arg2 | |
| (0) | =[] | y | i |
| (1) | := | x | (0) |
Трехадресный код может быть представлен не списком троек, а списком указателей на них. Такая реализация обычно называется косвенными тройками. Например, тройки рис. таблица 8.2б, могут быть реализованы так, как это изображено на рис. рис. 8.3.

Рис. 8.3.
При генерации объектного кода каждой переменной, как временной, так и определенной в исходной программе, назначается память периода исполнения, адрес которой обычно хранится в таблице генератора кода. При использовании четверок этот адрес легко получить через эту таблицу.
Более существенно преимущество четверок проявляется в оптимизирующих компиляторах, когда может возникнуть необходимость перемещать операторы. Если перемещается оператор, вычисляющий x, не требуется изменений в операторе, использующем x. В записи же тройками перемещение оператора, определяющего временное значение, требует изменения всех ссылок на этот оператор в массивах arg1 и arg2. Из-за этого тройки трудно использовать в оптимизирующих компиляторах.
В случае применения косвенных троек оператор может быть перемещен переупорядочиванием списка операторов. При этом не надо менять указатели на op, arg1 и arg2. Этим косвенные тройки похожи на четверки. Кроме того, эти два способа требуют примерно одинаковой памяти. Как и в случае простых троек, при использовании косвенных троек выделение памяти для временных значений может быть отложено на этап генерации кода. По сравнению с четверками при использование косвенных троек можно сэкономить память, если одно и то же временное значение используется более одного раза. Например, на рис. 8.3 можно объединить строки (14) и (16), после чего можно объединить строки (15) и (17).
Уровень промежуточного представления
Как видно из приведенных примеров, промежуточное представление программы может в различной степени быть близким либо к исходной программе, либо к машине. Например, промежуточное представление может содержать адреса переменных, и тогда оно уже не может быть перенесено на другую машину. С другой стороны, промежуточное представление может содержать раздел описаний программы, и тогда информацию об адресах можно извлечь из обработки описаний. В то же время ясно, что первое более эффективно, чем второе. Операторы управления в промежуточном представлении могут быть представлены в исходном виде (в виде операторов языка if, for, while и т.д.), а могут содержаться в виде переходов. В первом случае некоторая информация может быть извлечена из самой структуры (например, для оператора for - информация о переменной цикла, которую, может быть, разумно хранить на регистре, для оператора case - информация о таблице меток и т.д.).
Во втором случае представление проще и унифицированней. Некоторые формы промежуточного представления удобны для различного рода оптимизаций, некоторые - нет (например, косвенные тройки, в отличие от префиксной записи, позволяют эффективное перемещение кода).
Виртуальная машина Java
Программы на языке Java транслируются в специальное промежуточное представление, которое затем интерпретируется так называемой "виртуальной машиной Java ". Виртуальная машина Java представляет собой стековую машину: она не имеет памяти прямого доступа, все операции выполняются над операндами, расположенными на верхушке стека. Чтобы, например, выполнить операцию с участием константы или переменной, их предварительно необходимо загрузить на верхушку стека. Код операции - всегда один байт. Если операция имеет операнды, они располагаются в следующих байтах.
К элементарным типам данных, с которыми работает машина, относятся short, integer, long, float, double (все знаковые).
Атрибутная схема для алгоритма сопоставления образцов
Алгоритмы 9.5 и 9.6 являются "универсальными" в том смысле, что конкретные грамматики выражений и образцов являются, по-существу, параметрами этих алгоритмов. В то же время, для каждой конкретной грамматики можно написать свой алгоритм поиска образцов. Например, в случае нашей грамматики выражений и приведенных на рис. 9.25
образцов алгоритм 9.6 может быть представлен атрибутной грамматикой, приведенной ниже.
Наследуемый атрибут Match содержит упорядоченный список (вектор) образцов для сопоставления в поддереве данной вершины. Каждый из образцов имеет вид либо <op op-list> (op - операция в данной вершине, а op- list - список ее операндов), либо представляет собой нетерминал N. В первом случае op-list "распределяется" по потомкам вершины для дальнейшего сопоставления. Во втором случае сопоставление считается успешным, если есть правило N

Таким образом, при сопоставлении образцов могут встретиться два случая:
Вектор образцов содержит образец <op fPatig>, где op - операция, примененная в данной вершине. Тогда распределяем образцы Pati по потомкам и сопоставление по данному образцу считаем успешным (истинным), если успешны сопоставления элементов этого образца по всем потомкам.Образцом является нетерминал N. Тогда рассматриваем все правила вида N

Отметим, что в общем случае в потомки одновременно передается неско-лько образцов для сопоставления. В приведенной ниже атрибутной схеме не рассматриваются правила выбора покрытия наименьшей стоимости (см.
предыдущий раздел). Выбор оптимального покрытия может быть сделан еще одним проходом по дереву, аналогично тому, как это было сделано выше. Например, в правиле с '+' имеется несколько образцов для Reg, но реального выбора одного из них не осуществляется. Кроме того, не уточнены некоторые детали реализации. В частности, конкретный способ формирования векторов Match и Pattern. В тексте употребляется термин "добавить", что означает добавление к вектору образцов очередного элемента. Векторы образцов записаны в угловых скобках.
RULE Stat ::= '=' Reg Reg SEMANTICS Match<2>=<'+' Reg Const>; Match<3>=<Reg>; Pattern<0>[1]=Pattern<2>[1]&Pattern<3>[1].
Этому правилу соответствует один образец 2. Поэтому в качестве образцов потомков через их атрибуты Match передаются, соответственно, <'+' Reg Const> и <Reg>.
RULE Reg ::= '+' Reg Reg SEMANTICS if (Match<0> содержит Reg в позиции i) {Match<2>=<Reg,Reg,Reg>; Match<3>=<Const,Reg,<'@' '+' Reg Const>>; } if (Match<0> содержит образец <'+' Reg Const> в позиции j) {добавить Reg к Match<2> в некоторой позиции k; добавить Const к Match<3> в некоторой позиции k; } if (Match<0> содержит образец <'+' Reg Const> в позиции j) Pattern<0>[j]=Pattern<2>[k]&Pattern<3>[k]; if (Match[0] содержит Reg в i-й позиции) Pattern<0>[i]=(Pattern<2>[1]&Pattern<3>[1]) |(Pattern<2>[2]&Pattern<3>[2]) |(Pattern<2>[3]&Pattern<3>[3]).
Образцы, соответствующие этому правилу, следующие:
(4) Reg



Атрибутам Match второго и третьего символов в качестве образцов при сопоставлении могут быть переданы векторы <Reg, Reg, Reg> и <Const, Reg, <'@' '+' Reg Const>>, соответственно. Из анализа других правил можно заключить, что при сопоставлении образцов предков левой части данного правила атрибуту Match символа левой части может быть передан образец <'+' Reg Const> (из образцов 2, 3, 6) или образец Reg.
RULE Reg ::= '@' Reg SEMANTICS if (Match<0> содержит Reg в i-й позиции) Match<2>=<<'+' Reg Const>,Reg>; if (Match<0> содержит <'@' '+' Reg Const> в j-й позиции) добавить к Match<2> <'+' Reg Const> в k позиции; if (Match<0> содержит Reg в i-й позиции)
Pattern<0>[i]=Pattern<2>[1]|Pattern<2>[2]; if (Match<0> содержит <'@' '+' Reg Const> в j-й позиции) Pattern<0>[j]=Pattern<2>[k].
Образцы, соответствующие этому правилу, следующие:
(3) Reg


Соответственно, атрибуту Match второго символа в качестве образцов при сопоставлении могут быть переданы <'+' Reg Const> (образец 3) или <Reg> (образец 7). Из анализа других правил можно заключить, что при сопоставлении образцов предков левой части данного правила атрибуту Match могут быть переданы образцы <'@' '+' Reg Const> (из образца 6) и Reg.
RULE Reg ::= Const SEMANTICS if (Pattern<0> содержит Const в j-й позиции) Pattern<0>[j]=true; if (Pattern<0> содержит Reg в i-й позиции) Pattern<0>[i]=true.
Для дерева рис. 9.24 получим значения атрибутов, приведенные на рис. 9.28. Здесь M обозначает Match, P - Pattern, C - Const, R - Reg.

Рис. 9.28.
Динамическая организация памяти
Динамическая организация памяти - это организация памяти периода исполнения программы. Оперативная память программы обычно состоит из нескольких основных разделов: стек (магазин), куча, область статических данных (инициализированных и неинициализированных). Наиболее сложной является работа со стеком. Вообще говоря, стек периода исполнения необходим для программ не на всех языках программирования. Например, в ранних версиях Фортрана нет рекурсии, так что программа может исполняться без стека. С другой стороны, исполнение программы с рекурсией может быть реализовано и без стека (того же эффекта можно достичь, например, и с помощью списковых структур). Однако, для эффективной реализации пользуются стеком, который, как правило, поддерживается на уровне машинных команд.
Рассмотрим схему организации магазина периода выполнения для простейшего случая (как, например, в языке Паскаль), когда все переменные в магазине (фактические параметры и локальные переменные) имеют известные при трансляции смещения. Магазин служит для хранения локальных переменных (и параметров) и обращения к ним в языках, допускающих рекурсивные вызовы процедур. Еще одной задачей, которую необходимо решать при трансляции языков с блочной структурой - обеспечение реализации механизмов статической вложенности. Пусть имеется следующий фрагмент программы на Паскале:
procedure P1; var V1; procedure P2; var V2; begin ... P2; V1:=... V2:=... ... end; begin ... P2; ... end;
В процессе выполнения этой программы, находясь в процедуре P2, мы должны иметь доступ к последнему экземпляру значений переменных процедуры P2 и к экземпляру значений переменных процедуры P1, из которой была вызвана P2. Кроме того, необходимо обеспечить восстановление состояния программы при завершении выполнения процедуры.
Мы рассмотрим две возможные схемы динамической организации памяти: схему со статической цепочкой и с дисплеем в памяти. В первом случае все статические контексты связаны в список, который называется статической цепочкой; в каждой записи для процедуры в магазине хранится указатель на запись статически охватывающей процедуры (помимо, конечно, указателя динамической цепочки - указателя на "базу" динамически предыдущей процедуры). Во втором случае для хранения ссылок на статические контексты используется массив, называемый дисплеем. Использование той или иной схемы определяется, помимо прочих условий, прежде всего числом адресных регистров.
Единичное наследование и виртуальные функции
Если класс base содержит виртуальную функцию vf, а класс derived, порожденный по классу base, также содержит функцию vf того же типа, то обращение к vf для объекта класса derived вызывает derived :: vf даже при доступе через указатель или ссылку на base. В таком случае говорят, что функция производного класса подменяет (override) функцию базового класса. Если, однако, типы этих функций различны, то функции считаются различными и механизм виртуальности не включается.
Виртуальные функции можно реализовать при помощи таблицы указателей на виртуальные функции vtbl. В случае единичного наследования таблица виртуальных функций класса будет содержать ссылки на соответствующие функции, а каждый объект данного класса будет содержать указатель на таблицу vtbl.
class A { public: int a; virtual void f(int); virtual void g(int); virtual void h(int); }; class B : public A { public: int b; void g(int); }; class C : public B { public: int c; void h(int); };
Объект класса C будет выглядеть примерно так:

Рис. 9.20.
Генерация кода
Задача генератора кода - построение для программы на входном языке эквивалентной машинной программы. Обычно в качестве входа для генератора кода служит некоторое промежуточное представление программы.
Генерация кода включает ряд специфических, относительно независимых подзадач: распределение памяти (в частности, распределение регистров), выбор команд, генерацию объектного (или загрузочного) модуля. Конечно, независимость этих подзадач относительна: например, при выборе команд нельзя не учитывать схему распределения памяти, и, наоборот, схема распределения памяти (регистров, в частности) ведет к генерации той или иной последовательности команд. Однако удобно и практично эти задачи все же разделять, обращая при этом внимание на их взаимодействие.
В какой-то мере схема генератора кода зависит от формы промежуточного представления. Ясно, что генерация кода из дерева отличается от генерации кода из троек, а генерация кода из префиксной записи отличается от генерации кода из ориентированного графа. В то же время все генераторы кода имеют много общего, и основные применяемые алгоритмы отличаются, как правило, только в деталях, связанных с используемым промежуточным представлением.
В дальнейшем в качестве промежуточного представления мы будем использовать префиксную нотацию. А именно, алгоритмы генерации кода будем излагать в виде атрибутных схем со входным языком Лидер.
Множественное наследование
Имея два класса
class A {. . . af (int);} class B {. . . bf (int); }
можно объявить третий класс с этими двумя в качестве базовых:
class C : public A, public B {. . . }
Объект класса C может быть размещен как непрерывный объект вида:

Рис. 9.17.
Как и в случае с единичным наследованием, здесь не гарантируется порядок выделения памяти для базовых классов, поэтому объект класса C может выглядеть и так:

Рис. 9.18.
Доступ к члену класса A, B или C реализуется в точности так же, как и для единичного наследования: компилятор знает положение в объекте каждого члена и порождает соответствующий код.
Если объект размещен в памяти в соответствии с первой диаграммой: сначала часть A объекта, а затем части B и C, то вызов функции - члена класса A или C будет таким же, как вызов функции-члена при единичном наследовании. Вызов функции-члена класса B для объекта, заданного указателем на C, реализуется несколько сложнее. Рассмотрим
C* pc = new C; pc

Функция B :: bf() естественно предполагает, что ее параметр this является указателем на B. Чтобы получить указатель на часть B объекта C, следует добавить к указателю pc смещение B относительно C - константу времени компиляции, которую мы будем называть delta(B). Соотношение указателя pc и указателя this, передаваемого в B::bf, показано ниже.

Рис. 9.19.
Множественное наследование и виртуальные функции
При множественном наследовании виртуальные функции реализуются несколько сложнее. Рассмотрим следующие объявления:
class A { public: virtual void f(int); }; class B : { public: virtual void f(int); virtual void g(int); }; class C : public A, public B { public: void f(); };
Поскольку класс A порожден по классам A и B, каждый из следующих вызовов будет обращаться к C :: f() (считая, что каждый из трех указателей смотрит на объект класса C):
pa



Рассмотрим, для примера, вызов pb

Следовательно, delta(B) должно где-то храниться и быть доступно во время исполнения. Поскольку это смещение нужно только для виртуального вызова функции, логично хранить его в таблице виртуальных функций.
Указатель this, передаваемый виртуальной функции, может быть вычислен путем вычитания смещения объекта, для которого была определена виртуальная функция, из смещения объекта, для которого она вызвана, а затем вычитания этой разности из указателя, используемого при вызове. Здесь значение delta(B) будет необходимо для поиска начала объекта (в нашем случае C), содержащего B, по указателю на B. Сгенерированный код вычтет значение delta(B) из значения указателя, так что хранится смещение со знаком минус, -delta(B). Объект класса C будет выглядеть следующим образом:

Рис. 9.21.
Таблица виртуальных функций vtbl для B в C отличается от vtbl для отдельно размещенного B. Каждая комбинация базового и производного классов имеет свою таблицу vtbl. В общем случае объект производного класса требует таблицу vtbl для каждого базового класса плюс таблицу для производного класса, не считая того, что производный класс может разделять таблицу vtbl со своим первым базовым классом. Таким образом, для объекта типа C в этом примере требуется две таблицы vtbl (таблица для A в C объединена с таблицей для C oбъекта и еще одна таблица нужна для B объекта в C).
Модель машины
При изложении алгоритмов генерации кода мы будем следовать некоторой модели машины, в основу которой положена система команд микропроцессора Motorola MC68020. В микропроцессоре имеется регистр - счетчик команд PC, 8 регистров данных и 8 адресных регистров.
В системе команд используются следующие способы адресации:
ABS - абсолютная: исполнительным адресом является значение адресного выражения.
IMM - непосредственный операнд: операндом команды является константа, заданная в адресном выражении.
D - прямая адресация через регистр данных, записывается как Хn, операнд находится в регистре Хn.
А - прямая адресация через адресный регистр, записывается как An, операнд находится в регистре An.
INDIRECT - записывается как (An), адрес операнда находится в адресном регистре An.
POST - пост-инкрементная адресация, записывается как (Аn)+, исполнительный адрес есть значение адресного регистра An и после исполнения команды значение этого регистра увеличивается на длину операнда.
PRE - преинкрементная адресация, записывается как -(Аn): перед исполнением операции содержимое адресного регистра An уменьшается на длину операнда, исполнительный адрес равен новому содержимому адресного регистра.
INDISP - косвенная адресация со смещением, записывается как (bd,An), исполнительный адрес вычисляется как (An)+d - содержимое An плюс d.
INDEX - косвенная адресация с индексом, записывается как (bd,An, Xn*sc), исполнительный адрес вычисляется как (An)+bd+(Xn)*sc - содержимое адресного регистра + адресное смещение + содержимое индексного регистра, умноженное на sc.
INDIRPC - косвенная через PC (счетчик команд), записывается как (bd, PC), исполнительный адрес определяется выражением (PC)+bd.
INDEXPC - косвенная через PC со смещением, записывается как (bd,PC, Xn*sc), исполнительный адрес определяется выражением (PC)+bd+(Xn)*sc.
INDPRE - пре-косвенная через память, записывается как ([bd,An,sc*Xn], od) (схема вычисления адресов для этого и трех последующих способов адресации приведена ниже).
INDPOST - пост-косвенная через память: ([bd,An],sc*Xn,od).
INDPREPC - прекосвенная через PC: ([bd,PC,sc*Xn],od).
INDPOSTPC - пост-косвенная через PC: ([bd,PC],Xn,od). Здесь bd - это 16- или 32- битная константа, называемая смещением, od - 16- или 32-битная литеральная константа, называемая внешним смещением. Эти способы адресации могут использоваться в упрощенных формах без смещений bd и/или od и без регистров An или Xn. Следующие примеры иллюстрируют косвенную постиндексную адресацию:
MOVE D0, ([A0]) MOVE D0, ([4,A0]) MOVE D0, ([A0],6) MOVE D0, ([A0],D3) MOVE D0, ([A0],D4,12) MOVE D0, ([$12345678,A0],D4,$FF000000)
Индексный регистр Xn может масштабироваться (умножаться) на 2,4,8, что записывается как sc*Xn. Например, в исполнительном адресе ([24,A0, 4*D0]) содержимое квадратных скобок вычисляется как [A0] + 4 * [D0] + 24.
Эти способы адресации работают следующим образом. Каждый исполнительный адрес содержит пару квадратных скобок [...] внутри пары круглых скобок, то есть ([...], ... ). Сначала вычисляется содержимое квадратных скобок, в результате чего получается 32-битный указатель. Например, если используется постиндексная форма [20,A2], то исполнительный адрес - это 20 + [A2]
Аналогично, для преиндексной формы [12,A4,D5] исполнительный адрес - это 12 + [A4] + [D5]. Указатель, сформированный содержимым квадратных скобок, используется для доступа в память, чтобы получить новый указатель (отсюда термин косвенная адресация через память). К этому новому указателю добавляется содержимое внешних круглых скобок и таким образом формируется исполнительный адрес операнда.
В дальнейшем изложении будут использованы следующие команды (в частности, рассматриваются только арифметические команды с целыми операндами, но не с плавающими):
MOVEA ИА, А - загрузить содержимое по исполнительному адресу ИА на адресный регистр А.
MOVE ИА1, ИА2 - содержимое по исполнительному адресу ИА1 переписать по исполнительному адресу ИА2.
MOVEM список_регистров, ИА - сохранить указанные регистры в памяти, начиная с адреса ИА (регистры указываются маской в самой команде).
MOVEM ИА, список_регистров - восстановить указанные регистры из памяти, начиная с адреса ИА (регистры указываются маской в самой команде).
LEA ИА, А - загрузить исполнительный адрес ИА на адресный регистр А.
MUL ИА, D - умножить содержимое по исполнительному адресу ИА на содержимое регистра данных D и результат разместить в D (на самом деле в системе команд имеются две различные команды MULS и MULU для чисел со знаком и чисел без знака соответственно; для упрощения мы не будем принимать во внимание это различие).
DIV ИА, D - разделить содержимое регистра данных D на содержимое по исполнительному адресу ИА и результат разместить в D.
ADD ИА, D - сложить содержимое по исполнительному адресу ИА с содержимым регистра данных D и результат разместить в D.
SUB ИА, D - вычесть содержимое по исполнительному адресу ИА из содержимого регистра данных D и результат разместить в D.
Команды CMP и TST формируют разряды регистра состояний. Всего имеется 4 разряда: Z - признак нулевого результата, N - признак отрицательного результата, V - признак переполнения, C - признак переноса.
CMP ИА, D - из содержимого регистра данных D вычитается содержимое по исполнительному адресу ИА, при этом формируется все разряды регистра состояний, но содержимое регистра D не меняется.
TST ИА - выработать разряд Z регистра состояний по значению, находящемуся по исполнительному адресу ИА.
BNE ИА - условный переход по признаку Z = 1 (не равно) по исполнительному адресу ИА.
BEQ ИА - условный переход по признаку Z = 0 (равно) по исполнительному адресу ИА.
BLE ИА - условный переход по признаку N or Z (меньше или равно) по исполнительному адресу ИА.
BGT ИА - условный переход по признаку not N (больше) по исполнительному адресу ИА.
BLT ИА - условный переход по признаку N (меньше) по исполнительному адресу ИА.
BRA ИА - безусловный переход по адресу ИА.
JMP ИА - безусловный переход по исполнительному адресу.
RTD размер_локальных - возврат из подпрограммы с указанием размера локальных.
LINK A, размер_локальных - в стеке сохраняется значение регистра А, в регистр А заносится указатель на это место в стеке и указатель стека продвигается на размер локальных.
UNLK A - стек сокращается на размер локальных и регистр А восстанавливается из стека.
Назначение адресов
Назначение адресов переменным, параметрам и полям записей происходит при обработке соответствующих объявлений. В однопроходном трансляторе это может производиться вместе с построением основной таблицы символов и соответствующие адреса (или смещения) могут храниться в этой же таблице. В промежуточном представлении Лидер объявления сохранены, что делает это промежуточное представление машинно-независимым. Напомним, что в Лидер-представлении каждому описанию соответствует некоторый номер. В процессе работы генератора кодов поддерживается таблица Table, в которой по этому номеру (входу) содержится следующая информация:
для типа: его размер;для переменной: смещение в области процедуры (или глобальной области);для поля записи: смещение внутри записи;для процедуры: размер локальных параметров;для массива: размер массива, размер элемента, значение левой и правой границы.
Для вычисления адресов определим для каждого объявления два синтезируемых атрибута: DISP будет обозначать смещение внутри области процедуры (или единицы компиляции), а SIZE - размер. Тогда семантика правила для списка объявлений принимает вид
RULE DeclPart ::= ( Decl ) SEMANTICS Disp<1>=0; 1A: Disp<1>=Disp<1>+Size<1>; Size<0>=Disp<1>.
Все объявления, кроме объявлений переменных, имеют нулевой размер. Размер объявления переменной определяется следующим правилом:
RULE Decl ::= 'VAR' TypeDes SEMANTICS Tablentry Entry; 0: Entry=IncTab; Size<0>=((Table[VAL<2>]+1) / 2)*2; // Выравнивание на границу слова Table[Entry]=Disp<0>+Size<0>.
В качестве примера трансляции определения типа рассмотрим обработку описания записи:
RULE TypeDes ::= 'REC' ( TypeDes ) 'END' SEMANTICS int Disp; Tablentry Temp; 0: Entry<0>=IncTab; Disp=0; 2A: {Temp=IncTab; Table[Temp]=Disp; Disp=Disp+Table[Entry<2>]+1) / 2)*2; // Выравнивание на границу слова } Table[Entry<0>]=Disp.
Организация магазина с дисплеем
Рассмотрим теперь организацию магазина с дисплеем. Дисплей - это массив (DISPLAY) , i-й элемент которого представляет собой указатель на область активации последней вызванной подпрограммы i-го статического уровня. Доступ к переменным самой внутренней подпрограммы осуществляется через регистр BP. Дисплей может быть реализован либо через регистры (если их достаточно), либо через массив в памяти.
При вызове процедуры следующего (по отношению к вызывающей) уровня в дисплее отводится очередной элемент. Если вызывающая процедура имеет статический уровень i, то при вызове процедуры уровня j

Иногда используется комбинированная схема - дисплей в магазине. Дисплей хранится в области активации каждой процедуры. Формирование дисплея для процедуры осуществляется в соответствии с правилами, описанными выше.
Отдельного рассмотрения требует вопрос о технике передачи фактических параметров. Конечно, в случае простых параметров (например, чисел) проблем не возникает. Однако передача массивов по значению - операция довольно дорогая, поэтому с точки зрения экономии памяти целесообразнее сначала в подпрограмму передать адрес массива, а затем уже из подпрограммы по адресу передать в магазин сам массив. В связи с передачей параметров следует упомянуть еще одно обстоятельство.
Рассмотренная схема организации магазина допустима только для языков со статически известными размерами фактических параметров. Однако, например, в языке Модула-2 по значению может быть передан гибкий массив, и в этом случае нельзя статически распределить память для параметров. Обычно в таких случаях заводят так называемый "паспорт" массива, в котором хранится вся необходимая информация, а сам массив размещается в магазине в рабочей области выше сохраненных регистров.
Организация магазина со статической цепочкой
Итак, в случае статической цепочки магазин организован, как это изображено на рис. 9.1.
Таким образом, на запись текущей процедуры в магазине указывает регистр BP (Base Pointer), с которого начинается динамическая цепочка. На статическую цепочку указывает регистр LP (Link Pointer). В качестве регистров BP и LP в различных системах команд могут использоваться

Рис. 9.1.
универсальные, адресные или специальные регистры. Локальные переменные отсчитываются от регистра BP вверх, фактические параметры - вниз с учетом памяти, занятой точкой возврата и самим сохраненным регистром BP. Вызов подпрограмм различного статического уровня производится несколько поразному. При вызове подпрограммы того же статического уровня, что и вызывающая подпрограмма (например, рекурсивный вызов той же самой подпрограммы), выполняются следующие команды:
Занесение фактических параметров в магазин
JSR A
Команда JSR A продвигает указатель SP, заносит PC на верхушку магазина и осуществляет переход по адресу A. После выполнения этих команд состояние магазина становится таким, как это изображено на рис. 9.2. Занесение BP, отведение локальных, сохранение регистров делает вызываемая подпрограмма (см. ниже).

Рис. 9.2.
При вызове локальной подпрограммы необходимо установить указатель статического уровня на текущую подпрограмму, а при выходе - восстановить его на старое значение (охватывающей текущую). Для этого исполняются следующие команды:
Синтаксический анализ для T-грам- матик
Обычно код генерируется из некоторого промежуточного языка с довольно жесткой структурой. В частности, для каждой операции известна ее размерность, то есть число операндов, большее или равное 0. Операции задаются терминальными символами, и наоборот - будем считать все терминальные символы знаками операций. Назовем грамматики, удовлетворяющие этим ограничениям, T-грам- матиками. Правая часть каждой продукции в Т-грамматике есть правильное префиксное выражение, которое может быть задано следующим определением:
Операция размерности 0 является правильным префиксным выражением;Нетерминал является правильным префиксным выражением;Префиксное выражение, начинающееся со знака операции размерности n > 0, является правильным, если после знака операции следует n правильных префиксных выражений;Ничто другое не является правильным префиксным выражением
Образцы, соответствующие машинным командам, задаются правилами грамматики (вообще говоря, неоднозначной). Генератор кода анализирует входное префиксное выражение и строит одновременно все возможные деревья разбора. После окончания разбора выбирается дерево с наименьшей стоимостью. Затем по этому единственному оптимальному дереву генерируется код.
Для T-грамматик все цепочки, выводимые из любого нетерминала A, являются префиксными выражениями с фиксированной арностью операций. Длины всех выражений из входной цепочки a1 ... an можно предварительно вычислить (под длиной выражения имеется ввиду длина подстроки, начинающейся с символа кода операции и заканчивающейся последним символом, входящим в выражение для этой операции). Поэтому можно проверить, сопоставимо ли некоторое правило с подцепочкой ai : : : ak входной цепочки a1 ... an, проходя слева-направо по ai ... ak. В процессе прохода по цепочке предварительно вычисленные длины префиксных выражений используются для того, чтобы перейти от одного терминала к следующему терминалу, пропуская подцепочки, соответствующие нетерминалам правой части правила.
Цепные правила не зависят от операций, следовательно, их необходимо проверять отдельно.
Применение одного цепного правила может зависеть от применения другого цепного правила. Следовательно, применение цепных правил необходимо проверять до тех пор, пока нельзя применить ни одно из цепных правил. Мы предполагаем, что в грамматике нет циклов в применении цепных правил. Построение всех вариантов анализа для T-грамматики дано ниже в алгоритме 9.5. Тип Titem в алгоритме 9.5 ниже служит для описания ситуаций (то есть правил вывода и позиции внутри правила). Тип Tterminal - это тип терминального символа грамматики, тип Tproduction - тип для правила вывода.
Листинг 9.5.
(html, txt)
Проверить, принадлежит ли (S->w) множеству r[0]; Множества r[i] имеют размер O(|P|). Можно показать, что алгоритм имеет временную и емкостную сложность O(n). Рассмотрим вновь пример рис. 9.24. В префиксной записи приведенный фрагмент программы записывается следующим образом:
= + a x + @ + + b y @ + i z 5
На рис. 9.27 приведен результат работы алгоритма. Правила вычисления стоимости приведены в следующем разделе. Все возможные выводы входной цепочки (включая оптимальный) можно построить, используя таблицу l длин префиксных выражений и таблицу r применимых правил. Операция Длина Правила (стоимость)

Рис. 9.27.
Сопоставление образцов
Техника генерации кода, рассмотренная выше, основывалась на однозначном соответствии структуры промежуточного представления и описывающей это представление грамматики. Недостатком такого "жесткого" подхода является то, что как правило одну и ту же программу на промежуточном языке можно реализовать многими различными способами в системе команд машины. Эти разные реализации могут иметь различную длину, время выполнения и другие характеристики. Для генерации более качественного кода может быть применен подход, изложенный в настоящей главе.
Этот подход основан на понятии "сопоставления образцов": командам машины сопоставляются некоторые "образцы", вхождения которых ищутся в промежуточном представлении программы, и делается попытка "покрыть" промежуточную программу такими образцами. Если это удается, то по образцам восстанавливается программа уже в кодах. Каждое такое покрытие соответствует некоторой программе, реализующей одно и то же промежуточное представление.
На рис. 9.24 показано промежуточное дерево для

Рис. 9.24.
оператора a = b[i] + 5, где a, b, i - локальные переменные, хранимые со смещениями x, y, z соответственно в областях данных с одноименными адресами.
Элемент массива b занимает память в одну машинную единицу. 0-местная операция const возвращает значение атрибута соответствующей вершины промежуточного дерева, указанного на рисунке в скобках после оператора. Одноместная операция @ означает косвенную адресацию и возвращает содержимое регистра или ячейки памяти, имеющей адрес, задаваемый аргументом операции.
На рис. 9.25 показан пример сопоставления образцов машинным командам. Приведены два варианта задания образца: в виде дерева и в виде правила контекстно-свободной грамматики. Для каждого образца указана машинная команда, реализующая этот образец, и стоимость этой команды.
В каждом дереве-образце корень или лист может быть

Рис. 9.25.
помечен терминальным и/или нетерминальным символом. Внутренние вершины помечены терминальными символами - знаками операций.
При наложении образца на дерево выражения, во-первых, терминальный символ образца должен соответствовать терминальному символу дерева, и, во-вторых, образцы должны "склеиваться" по типу нетерминального символа, то есть тип корня образца должен совпадать с типом вершины, в которую образец подставляется корнем. Допускается использование "цепных" образцов, то есть образцов, корню которых не соответствует терминальный символ, и имеющих единственный элемент в правой части. Цепные правила служат для приведения вершин к одному типу. Например, в рассматриваемой системе команд одни и те же регистры используются как для целей адресации, так и для вычислений. Если бы в системе команд для этих целей использовались разные группы регистров, то в грамматике команд могли бы использоваться разные нетерминалы, а для пересылки из адресного регистра в регистр данных могла бы использоваться соответствующая команда и образец.
Нетерминалы Reg на образцах могут быть помечены индексом (i или j), что (неформально) соответствует номеру регистра и служит лишь для пояснения смысла использования регистров. Отметим, что при генерации кода рассматриваемым методом не осуществляется распределение регистров. Это является отдельной задачей. Стоимость может определяться различными способами, например числом обращений к памяти при выборке и исполнении команды. Здесь мы не рассматриваем этого вопроса. На рис. 9.26 приведен пример покрытия промежуточного дерева рис. 9.24 образцами рис. 9.25. В рамки заключены фрагменты дерева, сопоставленные образцу правила, номер которого указывается в левом верхнем углу рамки. В квадратных скобках указаны результирующие вершины.
Приведенное покрытие дает такую последовательность команд:
1 MOVE #b,Rb 4 ADD #y,Rb 1 MOVE #i,Ri 6 ADD #z(Ri),Rb 7 MOVE (Rb),Rb 4 ADD #5,Rb
1 MOVE #a,Ra

Рис. 9.26.
2 MOVE Rb,#x(Ra)
Основная идея подхода заключается в том, что каждая команда машины описывается в виде такого образца. Различные покрытия дерева промежуточного представления соответствуют различным последовательностям машинных команд.Задача выбора команд состоит в том, чтобы выбрать наилучший способ реализации того или иного действия или последовательности действий, то есть выбрать в некотором смысле оптимальное покрытие.
Для выбора оптимального покрытия было предложено несколько интересных алгоритмов, в частности использующих динамическое программирование [14, 16]. Мы здесь рассмотрим алгоритм [15], комбинирующий возможности синтаксического анализа и динамического программирования. В основу этого алгоритма положен синтаксический анализ неоднозначных грамматик (модифицированный алгоритм Кока, Янгера и Касами [18, 19]), эффективный в реальных приложениях. Этот же метод может быть применен и тогда, когда в качестве промежуточного представления используется дерево.
Трансляция арифметических выражений
Одной из важнейших задач при генерации кода является распределение регистров. Рассмотрим хорошо известную технику распределения регистров при трансляции арифметических выражений, называемую алгоритмом Сети-Ульмана. (Замечание: в целях большей наглядности, в данном параграфе мы немного отступаем от семантики арифметических команд MC68020 и предполагаем, что команда
Op Arg1, Arg2
выполняет действие Arg2:=Arg1 Op Arg2.)
Пусть система команд машины имеет неограниченное число универсальных регистров, в которых выполняются арифметические команды. Рассмотрим, как можно сгенерировать код, используя для данного арифметического выражения минимальное число регистров.
Пусть имеется синтаксическое дерево выражения. Предположим сначала, что распределение регистров осуществляется по простейшей схеме сверху-вниз слева- направо, как изображено на рис. 9.5. Тогда к моменту генерации кода для поддерева LR занято n регистров. Пусть поддерево L требует nl регистров, а поддерево R - nr регистров. Если nl = nr, то при вычислении L будет использовано nl регистров и под результат будет занят (n+1)-

Рис. 9.5.
й регистр. Еще nr(= nl) регистров будет использовано при вычислении R. Таким образом, общее число использованных регистров будет равно n + nl + 1.
Если nl > nr, то при вычислении L будет использовано nl регистров. При вычислении R будет использовано nr < nl
регистров, и всего будет использовано не более чем n + nl
регистров. Если nl < nr, то после вычисления L под результат будет занят один регистр (предположим, (n + 1)-й) и nr регистров будет использовано для вычисления R. Всего будет использовано n + nr + 1 регистров.
Видно, что для деревьев, совпадающих с точностью до порядка потомков каждой вершины, минимальное число регистров при распределении их слева-направо достигается на дереве, у которого в каждой вершине слева расположено более "сложное" поддерево, требующее большего числа регистров. Таким образом, если дерево таково, что в каждой внутренней вершине правое поддерево требует меньшего числа регистров, чем левое, то, обходя дерево слева направо, можно оптимально распределить регистры.
Без перестройки дерева это означает, что если в некоторой вершине дерева справа расположено более сложное поддерево, то сначала сгенерируем код для него, а затем уже для левого поддерева.
Алгоритм работает следующим образом. Сначала осуществляется разметка синтаксического дерева по следующим правилам.
Правила разметки:
если вершина - правый лист или дерево состоит из единственной вершины, помечаем эту вершину числом 1, если вершина - левый лист, помечаем ее 0 (рис. 9.6).

Рис. 9.6.
если вершина имеет прямых потомков с метками l1 и l2, то в качестве метки этой вершины выбираем наибольшее из чисел l1 или l2 либо число l1 + 1, если l1 = l2 (рис. 9.6.).

Рис. 9.7.
Эта разметка позволяет определить, какое из поддеревьев требует большего количества регистров для своего вычисления. Далее осуществляется распределение регистров для результатов операций по следующим правилам:
Корню назначается первый регистр.Если метка левого потомка меньше метки правого, то левому потомку назначается регистр на единицу больший, чем предку, а правому - с тем же номером (сначала вычисляется правое поддерево и его результат помещается в регистр R), так что регистры занимаются последовательно. Если же метка левого потомка больше или равна метке правого потомка, то наоборот, правому потомку назначается регистр на единицу больший, чем предку, а левому - с тем же номером (сначала вычисляется левое поддерево и его результат помещается в регистр R - рис. 9.7).
После этого формируется код по следующим правилам:
если вершина - правый лист с меткой 1, то ей соответствует код
MOVE X, R
где R - регистр, назначенный этой вершине, а X - адрес переменной, связанной с вершиной (рис. 9.8, б);

Рис. 9.8.
если вершина внутренняя и ее левый потомок - лист с меткой 0, то ей соответствует код
Код правого поддерева Op X, R
где R - регистр, назначенный этой вершине, X - адрес переменной, связанной с вершиной, а Op - операция, примененная в вершине (рис. 9.8, а); если непосредственные потомки вершины не листья и метка правой вершины больше или равна метки левой, то вершине соответствует код
Код правого поддерева Код левого поддерева Op R+1, R

Рис. 9.9.
где R - регистр, назначенный внутренней вершине, и операция Op, вообще говоря, не коммутативная (рис. 9.9, б); если непосредственные потомки вершины не листья и метка правой вершины меньше метки левой вершины, то вершине соответствует код
Код левого поддерева Код правого поддерева Op R, R+1 MOVE R+1, R
Последняя команда генерируется для того, чтобы получить результат в нужном регистре (в случае коммутативной операции ее операнды можно поменять местами и избежать дополнительной пересылки - рис. 9.9, а).
Рассмотрим атрибутную схему, реализующую эти правила генерации кода (для большей наглядности входная грамматика соответствует обычной инфиксной записи, а не Лидер-представлению). В этой схеме генерация кода происходит не непосредственно в процессе обхода дерева, как раньше, а из-за необходимости переставлять поддеревья код строится в виде текста с помощью операции конкатенации. Практически, конечно, это нецелесообразно: разумнее управлять обходом дерева непосредственно, однако для простоты мы будем пользоваться конкатенацией.
Листинг 9.1.
(html, txt)
Атрибутированное дерево для выражения A*B+C*(D+E) приведено на рис. 9.10. При этом будет сгенерирован следующий код:
MOVE B, R1 MUL A, R1 MOVE E, R2 ADD D, R2 MUL C, R2 ADD R1, R2 MOVE R2, R1
Приведенная атрибутная схема требует двух проходов по дереву выражения. Рассмотрим теперь другую атрибутную схему, в которой достаточно одного обхода для генерация

Рис. 9.10.
программы для выражений с оптимальным распределением регистров [9].
Пусть мы произвели разметку дерева разбора так же, как и в предыдущем алгоритме. Назначение регистров будем производить следующим образом.
Левому потомку всегда назначается регистр, равный его метке, а правому - его метке, если она не равна метке его левого брата, и метке + 1, если метки равны. Поскольку более сложное поддерево всегда вычисляется раньше более простого, его регистр результата имеет больший номер, чем любой регистр, используемый при вычислении более простого поддерева, что гарантирует правильность использования регистров.
Приведенные соображения реализуются следующей атрибутной схемой:
Листинг 9.2.
(html, txt)
Команды пересылки требуются для согласования номеров регистров, в которых осуществляется выполнение операции, с регистрами, в которых должен быть выдан результат. Это имеет смысл, когда эти регистры разные. Получиться это может из-за того, что по приведенной схеме результат выполнения операции всегда находится в регистре с номером метки, а метки левого и правого поддеревьев могут совпадать.
Для выражения A*B+C*(D+E) будет сгенерирован следующий код:
MOVE E, R1
ADD D, R1 MUL C, R1 MOVE R1, R2 MOVE B, R1 MUL A, R1 ADD R1, R2
В приведенных атрибутных схемах предполагалось, что регистров достаточно для трансляции любого выражения. Если это не так, приходится усложнять схему трансляции и при необходимости сбрасывать содержимое регистров в память (или магазин).
Трансляция целых выражений
Трансляция выражений различных типов управляется синтаксически благодаря наличию указателя типа перед каждой операцией. Мы рассмотрим некоторые наиболее характерные проблемы генерации кода для выражений.
Система команд МС68020 обладает двумя особенностями, сказывающимися на генерации кода для арифметических выражений (то же можно сказать и о генерации кода для выражений типа "множества"):
один из операндов выражения (правый) должен при выполнении операции находиться на регистре, поэтому если оба операнда не на регистрах, то перед выполнением операции один из них надо загрузить на регистр;система команд довольно "симметрична", то есть нет специальных требований к регистрам при выполнении операций (таких, например, как пары регистров или требования четности и т.д.).
Поэтому выбор команд при генерации арифметических выражений определяется довольно простыми таблицами решений. Например, для целочисленного сложения такая таблица приведена на рис. 9.4.

Рис. 9.4.
Здесь имеется в виду, что R - операнд на регистре, V - переменная или константа. Такая таблица решений должна также учитывать коммутативность операций.
RULE IntExpr ::= 'PLUS' IntExpr IntExpr SEMANTICS if (Address<2>.AddrMode!=D) && (Address<3>.AddrMode!=D) {Address<0>.AddrMode=D; Address<0>.Addreg=GetFree(RegSet<Block>); Emit2(MOVE,Address<2>,Address<0>); Emit2(ADD,Address<2>,Address<0>); } else if (Address<2>.AddrMode==D) {Emit2(ADD,Address<3>,Address<2>); Address<0>:=Address<2>); } else {Emit2(ADD,Address<2>,Address<3>); Address<0>:=Address<3>); }.
Трансляция логических выражений
Логические выражения, включающие логическое умножение, логическое сложение и отрицание, можно вычислять как непосредственно, используя таблицы истинности, так и с помощью условных выражений, основанных на следующих простых правилах:
A AND B эквивалентно if A then B else False,
A OR B эквивалентно if A then True else B.
Если в качестве компонент выражений могут входить функции с побочным эффектом, то, вообще говоря, результат вычисления может зависеть от способа вычисления. В некоторых языках программирования не оговаривается, каким способом должны вычисляться логические выражения (например, в Паскале), в некоторых требуется, чтобы вычисления производились тем или иным способом (например, в Модуле-2 требуется, чтобы выражения вычислялись по приведенным формулам), в некоторых языках есть возможность явно задать способ вычисления (Си, Ада). Вычисление логических выражений непосредственно по таблицам истинности аналогично вычислению арифметических выражений, поэтому мы не будем их рассматривать отдельно. Рассмотрим подробнее способ вычисления с помощью приведенных выше формул (будем называть его "вычислением с условными переходами"). Иногда такой способ рассматривают как оптимизацию вычисления логических выражений.
Рассмотрим следующую атрибутную грамматику со входным языком логических выражений:
RULE Expr ::= BoolExpr SEMANTICS FalseLab<1>=False; TrueLab<1>=True; Code<0>=Code<1>.
RULE BoolExpr ::= BoolExpr 'AND' BoolExpr SEMANTICS FalseLab<1>=FalseLab<0>; TrueLab<1>=NodeLab<3>; FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>; Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>.
RULE BoolExpr ::= BoolExpr 'OR' BoolExpr SEMANTICS FalseLab<1>=NodeLab<3>; TrueLab<1>=TrueLab<0>; FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>; Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>.
RULE BoolExpr ::= F SEMANTICS Code<0>=NodeLab<0> + ":" + "GOTO" + FalseLab<0>.
RULE BoolExpr ::= T SEMANTICS Code<0>=NodeLab<0> + ":" + "GOTO" + TrueLab<0>.
Здесь предполагается, что все вершины дерева занумерованы и номер вершины дает атрибут NodeLab. Метки вершин передаются, как это изображено на рис. 9.11.
Таким образом, каждому атрибутированному дереву в этой атрибутной грамматике сопоставляется код, полученный в результате обхода дерева сверху-вниз слева-направо

Рис. 9.11.
следующим образом. При входе в вершину BoolExpr генерируется ее номер, в вершине F генерируется текст GOTO значение атрибута FalseLab<0>, в вершине T - GOTO значение атрибута TrueLab<0>. Например, для выражения
F OR ( F AND T AND T ) OR T
получим атрибутированное дерево, изображенное на рис. 9.12, и код
1:7: GOTO 2 2:8:4:9: GOTO 3 5:10: GOTO 6 6: GOTO True 3: GOTO True True: ... False: ...
Эту линеаризованную запись можно трактовать как программу вычисления логического значения: каждая строка может быть помечена номером вершины и содержать либо переход на другую строку, либо переход на True или False, что соответствует значению выражения true или false. Будем говорить, что полученная программа вычисляет (или интерпретирует) значение выражения, если в результате ее выполнения (от первой строки) мы придем к строке, содержащей GOTO True или GOTO False.

Рис. 9.12.
Утверждение 9.1. В результате интерпретации поддерева с некоторыми значениями атрибутов FalseLab и TrueLab в его корне выполняется команда GOTO TrueLab, если значение выражения истинно, и команда GOTO FalseLab, если значение выражения ложно.
Доказательство. Применим индукцию по высоте дерева. Для деревьев высоты 1, соответствующих правилам
BoolExpr ::= F и BoolExpr ::= T,
справедливость утверждения следует из соответствующих атрибутных правил. Пусть дерево имеет высоту n > 1. Зависимость атрибутов для дизъюнкции и конъюнкции приведена на рис. 9.13.
Если для конъюнкции значение левого поддерева ложно и по индукции вычисление левого поддерева

Рис. 9.13.
завершается командой GOTO FalseLab<1>, то получаем, что вычисление всего дерева завершается командой перехода GOTO FalseLab<0> (= FalseLab<1>). Если же значение левого поддерева истинно, то его вычисление завершается командой перехода GOTO TrueLab<1> (= NodeLab<3>). Если значение правого поддерева ложно, то вычисление всего дерева завершается командой GOTO FalseLab<0> (= FalseLab<3>). Если же оно истинно, вычисление всего дерева завершается командой перехода GOTO TrueLab<0> (= TrueLab<3>). Аналогично - для дизъюнкции.
Утверждение 9.2. Для любого логического выражения, состоящего из констант, программа, полученная в результате обхода дерева этого выражения, завершается со значением логического выражения в обычной интерпретации, то есть осуществляется переход на True для значения, равного true, и переход на
метку False для значения false.
Доказательство. Это утверждение является частным случаем предыдущего. Его справедливость следует из того, что метки корня дерева равны соответственно TrueLab = True и FalseLab = False.
Добавим теперь новое правило в предыдущую грамматику:
RULE BoolExpr ::= Ident SEMANTICS Code<0>=NodeLab<0> + ":" + "if (" + Val<1> + "==T) GOTO" + TrueLab<0> + "else GOTO" + FalseLab<0>.
Тогда, например, для выражения A OR (B AND C AND D) OR E получим следующую программу:
1:7: if (A==T) GOTO True else GOTO 2 2:8:4:9: if (B==T) GOTO 5 else GOTO 3 5:10: if (C==T) GOTO 6 else GOTO 3 6: if (D==T) GOTO True else GOTO 3 3: if (E==T) GOTO True else GOTO False True: ... False: ...
При каждом конкретном наборе данных эта программа превращается в программу вычисления логического значения.
Утверждение 9.3. В каждой строке программы, сформированной предыдущей атрибутной схемой, одна из меток внутри условного оператора совпадает с меткой следующей строки.
Доказательство. Действительно, по правилам наследования атрибутов TrueLab и FalseLab, в правилах для дизъюнкции и конъюнкции либо атрибут FalseLab, либо атрибут TrueLab принимает значение метки следующего поддерева.
Кроме того, как значение FalseLab, так и значение TrueLab, передаются в правое поддерево от предка. Таким образом, самый правый потомок всегда имеет одну из меток TrueLab или FalseLab, равную метке правого брата соответствующего поддерева. Учитывая порядок генерации команд, получаем справедливость утверждения.
Дополним теперь атрибутную грамматику следующим образом:
Листинг 9.3.
(html, txt)
Правила наследования атрибута Sign приведены на рис. 9.14.

Рис. 9.14.
Программу желательно сформировать таким образом, чтобы else-метка была как раз меткой следующей вершины. Как это можно сделать, следует из следующего утверждения.
Утверждение 9.4. В каждой терминальной вершине, метка ближайшего правого для нее поддерева равна значению атрибута FalseLab этой вершины, тогда и только тогда, когда значение атрибута Sign этой вершины равно true, и наоборот, метка ближайшего правого для нее поддерева равна значению атрибута TrueLab этой вершины, тогда и только тогда, когда значение атрибута Sign равно false.
Доказательство. Действительно, если ближайшей общей вершиной является AND, то в левого потомка передается Node- Lab правого потомка в качестве TrueLab и одновременно Sign правого потомка равен true. Если же ближайшей общей вершиной является OR, то в левого потомка передается NodeLab правого потомка в качестве FalseLab и одновременно Sign правого потомка равен false. Во все же правые потомки значения TrueLab, FalseLab и Sign передаются из предка (за исключением правила для NOT, в котором TrueLab и FalseLab меняются местами, но одновременно на противоположный меняется и Sign).
Эти два утверждения (3 и 4) позволяют заменить последнее правило атрибутной грамматики следующим образом:
RULE BoolExpr ::= Ident SEMANTICS Code<0>=NodeLab<0> + ":" + (Sign<0> ? "if (" + Val<1> + "==T) GOTO" + TrueLab<0> : "if (" + Val<1> + "==F) GOTO" + FalseLab<0>).
В свою очередь, при генерации машинных команд это правило можно заменить на следующее:
RULE BoolExpr ::= Ident SEMANTICS Code<0>=NodeLab<0> + ":" + "TST" + Val<1> + (Sign<0> ? "BNE" + TrueLab<0> : "BEQ" + FalseLab<0>).
Таким образом, для выражения A OR (B AND C AND D) OR E получим следующий код на командах перехода:
1:7: TST A BNE True 2:8:4:9: TST B BEQ 3 5:10: TST C BEQ 3 6: TST D BNE True 3: TST E BEQ False True: ... False: ...
Если элементом логического выражения является сравнение, то генерируется команда, соответствующая знаку сравнения (BEQ для =, BNE для <>, BGE для >= и т.д.), если атрибут Sign соответствующей вершины имеет значение true, и отрицание (BNE для =, BEQ для <>, BLT для >= и т.д.), если атрибут Sign имеет значение false.
Трансляция объектно-ориен- тированных свойств языков программирования
В этом разделе будут рассмотрены механизмы трансляции базовых конструкций объектно-ориентированных языков программирования, а именно наследования и виртуальных функций на примере языка С++.
Трансляция переменных
Переменные отражают все многообразие механизмов доступа в языке. Переменная имеет синтезированный атрибут ADDRESS - это запись, описывающая адрес в команде МС68020. Этот атрибут сопоставляется всем нетерминалам, представляющим значения. В системе команд МС68020 много способов адресации, и они отражены в структуре значения атрибута ADDRESS, имеющего следующий тип:
enum Register {D0,D1,D2,D3,D4,D5,D6,D7, A0,A1,A2,A3,A4,A5,A6,SP,NO};
enum AddrMode {D,A,Post,Pre,Indirect,IndPre,IndPost,IndirPC, IndPrePC,IndPostPC,InDisp,Index,IndexPC,Abs,Imm};
struct AddrType{ Register AddrReg,IndexReg; int IndexDisp,AddrDisp; short Scale; };
Значение регистра NO означает, что соответствующий регистр в адресации не используется.
Доступ к переменным осуществляется в зависимости от их уровня: глобальные переменные адресуются с помощью абсолютной адресации; переменные в процедуре текущего уровня адресуются через регистр базы А6.
Если стек организован с помощью статической цепочки, то переменные предыдущего статического уровня адресуются через регистр статической цепочки А5; переменные остальных уровней адресуются "пробеганием" по статической цепочке с использованием вспомогательного регистра. Адрес переменной формируется при обработке структуры переменной слева направо и передается сначала сверху вниз как наследуемый атрибут нетерминала VarTail, а затем передается снизу-вверх как глобальный атрибут нетерминала Variable. Таким образом, правило для обращения к переменной имеет вид (первое вхождение Number в правую часть - это уровень переменной, второе - ее Лидер-номер):
RULE Variable ::= VarMode Number Number VarTail SEMANTICS int Temp; struct AddrType AddrTmp1, AddrTmp2; 3: if (Val<2>==0) // Глобальная переменная {Address<4>.AddrMode=Abs; Address<4>.AddrDisp=0; } else // Локальная переменная {Address<4>.AddrMode=Index; if (Val<2>==Level<Block>) // Переменная // текущего уровня Address<4>.AddrReg=A6; else if (Val<2>==Level<Block>-1) // Переменная предыдущего уровня Address<4>.AddrReg=A5; else {Address<4>.Addreg= GetFree(RegSet<Block>); AddrTmp1.AddrMode=Indirect; AddrTmp1.AddrReg=A5; Emit2(MOVEA,AddrTmp1, Address<4>.AddrReg); AddrTmp1.AddrReg=Address<4>.AddrReg; AddrTmp2.AddrMode=A; AddrTmp2.AddrReg=Address<4>.AddrReg; for (Temp=Level<Block>-Val<2>; Temp>=2;Temp--) Emit2(MOVEA,AddrTmp1,AddrTmp2); } if (Val<2>==Level<Block>) Address<4>.AddrDisp=Table[Val<3>]; else Address<4>.AddrDisp= Table[Val<3>]+Table[LevelTab[Val<2>]]; }.
Функция GetFree выбирает очередной свободный регистр (либо регистр данных, либо адресный регистр) и отмечает его как использованный в атрибуте RegSet нетерминала Block. Процедура Emit2 генерирует двухадресную команду. Первый параметр этой процедуры - код команды, второй и третий параметры имеют тип AddrType и служат операндами команды. Смещение переменной текущего уровня отсчитывается от базы (А6), а других уровней - от указателя статической цепочки, поэтому оно определяется как алгебраическая сумма размера локальных параметров и величины смещения переменной. Таблица LevelTab - это таблица уровней процедур, содержащая указатели на последовательно вложенные процедуры.
Если стек организован с помощью дисплея, то трансляция для доступа к переменным может быть осуществлена следующим образом:
RULE Variable ::= VarMode Number Number VarTail SEMANTICS int Temp; 3: if (Val<2>==0) // Глобальная переменная {Address<4>.AddrMode=Abs; Address<4>.AddrDisp=0; } else // Локальная переменная {Address<4>.AddrMode=Index; if (Val<2>=Level<Block>) // Переменная // текущего уровня {Address<4>.AddrReg=A6; Address<4>.AddrDisp=Table[Val<3>]; } else {Address<4>.AddrMode=IndPost; Address<4>.AddrReg=NO; Address<4>.IndexReg=NO; Address<4>.AddrDisp=Display[Val<2>]; Address<4>.IndexDisp=Table[Val<3>]; } }.
Рассмотрим трансляцию доступа к полям записи. Она описывается следующим правилом (Number - это Лидер- номер описания поля):
RULE VarTail ::= 'FIL' Number VarTail SEMANTICS if (Address<0>.AddrMode==Abs) {Address<3>.AddrMode=Abs; Address<3>.AddrDisp= Address<0>.AddrDisp+Table[Val<2>]; } else {Address<3>=Address<0>; if (Address<0>.AddrMode==Index) Address<3>.AddrDisp= Address<0>.AddrDisp+Table[Val<2>]; else Address<3>.IndexDisp= Address<0>.IndexDisp+Table[Val<2>]; }.
Виртуальные базовые классы
К описателю базового класса можно добавить ключевое слово virtual. В этом случае единственный подобъект виртуального базового класса разделяется каждым базовым классом, в котором тот, исходный, базовый класс определен как виртуальный.
Пусть мы имеем следующую иерархию наследования:
class L {. . . } class A : public virtual L {. . . } class B : public virtual L {. . . } class C : public A, public B {. . . }
Это можно изобразить следующей диаграммой классов:

Рис. 9.15. Диаграмма классов
Каждый объект A или объект B будет содержать L, но в объекте C будет существовать лишь один объект класса L. Ясно, что представление объекта виртуального базового класса L не может быть в одной и той же позиции относительно и A, и B для всех объектов. Следовательно, во всех объектах классов, которые включают класс L как виртуальный базовый класс, должен храниться указатель на L. Реализация A, B и C объектов могла бы выглядеть следующим образом:

Рис. 9.16. Реализация A, B и C объектов
Виртуальные базовые классы с виртуальными функциями
При наличии виртуальных базовых классов построение таблиц для вызовов виртуальных функций становится более сложным. Рассмотрим следующие объявления:
class W { public: virtual void f(); virtual void g(); virtual void h(); virtual void k(); }; class MW : public virtual W { public: void g(); }; class BW : public virtual W { public: void f(); }; class BMW : public BW, public MW, public virtual W { public: void h(); };
Отношение наследования для этого примера может быть изображено в виде ациклического графа таким образом:

Рис. 9.22.
Функции-члены класса BMW могут использоваться, например, так:
void g(BMW¤pbmw) {pbmw ! f(); == вызывает BW :: f() pbmw ! g(); == вызывает MW :: g() pbmw ! h(); == вызывает BMW :: h() }
Рассмотрим теперь следующий вызов виртуальной функции f():
void h(BMW*pbmw) {MW*pmw = pbmw; pmw ! f(); == вызывает BW :: f(); потому, что // pbmw указывает на BMW, для которого f бер"тся из BW! }
Виртуальный вызов функции по одному пути в структуре наследования может привести к обращению к функции, переопределенной на другом пути.
Структура объектов класса BMW и его таблиц виртуальных функций vtbl могут выглядеть следующим образом:

Рис. 9.23.
Виртуальной функции должен быть передан указатель this на объект класса, в котором эта функция описана. Поэтому следует хранить смещение для каждого указателя функции из vtbl. Когда объект размещен в памяти так, как это изображено выше, смещение, хранимое с указателем виртуальной функции, исчисляется вычитанием смещения класса, для которого эта таблица vtbl создана, из смещения класса, поставляющего эту функцию. Рассмотрим пример:
void callvirt(w*pw) { pw ! f(); } main () { callvirt(new BMW); }
В функции main вызов callvirt с указателем на BMW требует приведения к указателю на W, поскольку функция callvirt ожидает параметр типа W*. Так как функция callvirt вызывает f() (через указатель на BMW, преобразованный к указателю на W), будет использована таблица vtbl класса W (в BMW), где указано, что экземпляром виртуальной функции f(), которую нужно вызвать, является BW :: f(). Чтобы передать функции BW :: f() указатель this на BW, указатель pw должен быть вновь приведен к указателю на BMW (вычитанием смещения для W), а затем к указателю на BW (добавлением смещения BW в объекте BMW). Значение смещения BW в объекте BMW минус смещение W в объекте BMW и есть смещение, хранимое в строке таблицы vtbl для w в BMW для функции BW :: f().
Выбор дерева вывода наименьшей стоимости
T-грамматики, описывающие системы команд, обычно являются неоднозначными. Чтобы сгенерировать код для некоторой входной цепочки, необходимо выбрать одно из возможных деревьев вывода. Это дерево должно представлять желаемое качество кода, например размер кода и/или время выполнения.
Для выбора дерева из множества всех построенных деревьев вывода можно использовать атрибуты стоимости, атрибутные формулы, вычисляющие их значения, и критерии стоимости, которые оставляют для каждого нетерминала единственное применимое правило. Атрибуты стоимости сопоставляются всем нетерминалам, атрибутные формулы - всем правилам T-грамматики.
Предположим, что для вершины n обнаружено применимое правило
p : A

где zi






a(A) = f(b(Xi), c(Xj),...) для 1


то производится вычисление значения атрибута a нетерминала A в вершине n. Для всех примененных правил ищется такое, которое дает минимальное значение стоимости. Отсутствие примененных правил обозначается через Undefined, значение которого полагается большим любого определенного значения.
Добавим в алгоритм 9.6 реализацию атрибутов стоимости, формул их вычисления и критериев отбора. Из алгоритма можно исключить поиск подвыводов, соответствующих правилам, для которых значение атрибута стоимости не определено. Структура данных, представляющая вершину дерева, принимает следующий вид:
Листинг 9.7.
(html, txt)
Процедура ВычислитьАтрибутыСтоимостиДля (A, n, (A

Процедура ПроверитьКритерийДля(C, n

Процедура Модифицировать(n


Выделение общих подвыражений
Выделение общих подвыражений относится к области оптимизации программ. В общем случае трудно (или даже невозможно) провести границу между оптимизацией и "качественной трансляцией". Оптимизация - это и есть качественная трансляция. Обычно термин "оптимизация" употребляют, когда для повышения качества программы используют ее глубокие преобразования такие, например, как перевод в графовую форму для изучения нетривиальных свойств программы.
В этом смысле выделение общих подвыражений - одна из простейших оптимизаций. Для ее осуществления требуется некоторое преобразование программы, а именно построение ориентированного ациклического графа, о котором говорилось в главе, посвященной промежуточным представлениям.
Линейный участок - это последовательность операторов, в которую управление входит в начале и выходит в конце без остановки и перехода изнутри.
Рассмотрим дерево линейного участка, в котором вершинами служат операции, а потомками - операнды. Будем говорить, что две вершины образуют общее подвыражение, если поддеревья для них совпадают, то есть имеют одинаковую структуру и, соответственно, одинаковые операции во внутренних вершинах и одинаковые операнды в листьях. Выделение общих подвыражений позволяет генерировать для них код один раз, хотя может привести и к некоторым трудностям, о чем вкратце будет сказано ниже.
Выделение общих подвыражений проводится на линейном участке и основывается на двух положениях.Выделение общих подвыражений проводится на линейном участке и основывается на двух положениях.
Поскольку на линейном участке переменной может быть несколько присваиваний, то при выделении общих подвыражений необходимо различать вхождения переменных до и после присваивания. Для этого каждая переменная снабжается счетчиком. Вначале счетчики всех переменных устанавливаются равными 0. При каждом присваивании переменной ее счетчик увеличивается на 1.Выделение общих подвыражений осуществляется при обходе дерева выражения снизу вверх слева направо.
При достижении очередной вершины (пусть операция, примененная в этой вершине, есть бинарная op; в случае унарной операции рассуждения те же) просматриваем общие подвыражения, связанные с op. Если имеется выражение, связанное с op и такое, что его левый операнд есть общее подвыражение с левым операндом нового выражения, а правый операнд - общее подвыражение с правым операндом нового выражения, то объявляем новое выражение общим с найденным и в новом выражении запоминаем указатель на найденное общее выражение. Базисом построения служит переменная: если операндами обоих выражений являются одинаковые переменные с одинаковыми счетчиками, то они являются общими подвыражениями. Если выражение не выделено как общее, оно заносится в список операций, связанных с op.
Рассмотрим теперь реализацию алгоритма выделения общих подвыражений. Поддерживаются следующие глобальные переменные:
Table - таблица переменных; для каждой переменной хранится ее счетчик (Count) и указатель на вершину дерева выражений, в которой переменная встретилась в последний раз в правой части (Last);
OpTable - таблица списков (типа LisType) общих подвыражений, связанных с каждой операцией. Каждый элемент списка хранит указатель на вершину дерева (поле Addr) и продолжение списка (поле List).
С каждой вершиной дерева выражения связана запись типа NodeType, со следующими полями:
Left - левый потомок вершины,
Right - правый потомок вершины,
Comm - указатель на предыдущее общее подвыражение,
Flag - признак, является ли поддерево общим подвыражением,
Varbl - признак, является ли вершина переменной,
VarCount - счетчик переменной. Выделение общих подвыражений и построение дерева осуществляются приведенными ниже правилами. Атрибут Entry нетерминала Variable дает указатель на переменную в таблице Table. Атрибут Val символа Op дает код операции. Атрибут Node символов IntExpr и Assignment дает указатель на запись типа NodeType соответствующего нетерминала.
Листинг 9.4.
(html, txt)
Рассмотрим теперь некоторые простые правила распределения регистров при наличии общих подвыражений.
Если число регистров ограничено, можно выбрать один из следующих двух вариантов.
При обнаружении общего подвыражения с подвыражением в уже просмотренной части дерева (и, значит, с уже распределенными регистрами) проверяем, расположено ли его значение на регистре. Если да, и если регистр после этого не менялся, заменяем вычисление поддерева на значение в регистре. Если регистр менялся, то вычисляем подвыражение заново.Вводим еще один проход. На первом проходе распределяем регистры. Если в некоторой вершине обнаруживается, что ее поддерево общее с уже вычисленным ранее, но значение регистра потеряно, то в такой вершине на втором проходе необходимо сгенерировать команду сброса регистра в рабочую память. Выигрыш в коде будет, если стоимость команды сброса регистра + доступ к памяти в повторном использовании этой памяти не превосходит стоимости заменяемого поддерева. Поскольку стоимость команды MOVE известна, можно сравнить стоимости и принять оптимальное решение: пометить предыдущую вершину для сброса либо вычислять поддерево полностью.
Система СУПЕР
Программа на входном языке СУПЕР ("метапрограмма") состоит из следующих разделов:
Заголовок;Раздел констант;Раздел типов;Алфавит;Раздел файлов;Раздел библиотеки;Атрибутная схема.
Заголовок определяет имя атрибутной грамматики, первые три буквы имени задают расширение имени входного файла для реализуемого транслятора. Раздел констант содержит описание констант, раздел типов - описание типов.
Алфавит содержит перечисление нетерминальных символов и классов лексем, а также атрибутов (и их типов), сопоставленных этим символам. Классы лексем являются терминальными символами с точки зрения синтаксического анализа, но могут иметь атрибуты, вычисляемые в процессе лексического анализа. Определение класса лексем состоит в задании имени класса, имен атрибутов для этого класса и типов этих атрибутов.
В разделе определения нетерминальных символов содержится перечисление этих символов с указанием приписанных им атрибутов и их типов. Аксиома грамматики указывается первым символом в списке нетерминалов. Раздел библиотеки содержит заголовки процедур и функций, используемых в формулах атрибутной грамматики. Раздел файлов содержит описание файловых переменных, используемых в формулах атрибутной грамматики. Файловые переменные можно рассматривать как атрибуты аксиомы.
Атрибутная схема состоит из списка синтаксических правил и сопоставленных им семантических правил. Для описания синтаксиса языка используется расширенная форма Бэкуса-Наура. Терминальные символы в правой части заключаются в кавычки, классы лексем и нетерминалы задаются их именами. Для задания в правой части необязательных символов используются скобки [ ], для задания повторяющихся конструкций используются скобки ( ). В этом случае может быть указан разделитель символов (после /). Например,
A ::= B [ C ] ( D ) ( E / ',' )
Первым правилом в атрибутной схеме должно быть правило для аксиомы.
Каждому синтаксическому правилу могут быть сопоставлены семантические действия. Каждое такое действие - это оператор, который может использовать атрибуты как символов данного правила (локальные атрибуты), так и символов, могущих быть предками (динамически) символа левой части данного правила в дереве разбора (глобальные атрибуты).
Для ссылки на локальные атрибуты символы данного правила (как терминальные, так и нетерминальные) нумеруются от 0 (для символа левой части). При ссылке на глобальные атрибуты надо иметь в виду, что атрибуты имеют области видимости на дереве разбора. Областью видимости атрибута вершины, помеченной N, является все поддерево N, за исключением его поддеревьев, также помеченных N.
Исполнение операторов семантической части правила привязывается к обходу дерева разбора сверху вниз слева направо. Для этого каждый оператор может быть помечен меткой, состоящей из номера ветви правила, к выполнению которой должен быть привязан оператор, и, возможно, одного из суффиксов A, B, E, M.
Суффикс A задает выполнение оператора перед каждым вхождением синтаксической конструкции, заключенной в скобки повторений ( ). Суффикс B задает выполнение оператора после каждого вхождения синтаксической конструкции, заключенной в скобки повторений ( ). Суффикс M задает выполнение оператора между вхождениями синтаксической конструкции, заключенной в скобки повторений ( ). Суффикс E задает выполнение оператора в том случае, когда конструкция, заключенная в скобки [ ], отсутствует.
Пример использование меток атрибутных формул:
D ::= 'd' => $0.y:=$0.x+1. A ::= B (C) [D] => $2.x:=1; 2M: $2.x:=$2.x+1; $3.x:=$2.x; 3E: $3.y:=$3.x; 3: writeln($3.y).
Процедура writeln напечатает число вхождений символа C в C-список, если D опущено. В противном случае напечатанное число будет на единицу больше.
Система YACC
В основу системы YACC положен синтаксический анализатор типа LALR(1), генерируемый по входной (мета) программе. Эта программа состоит из трех частей:
%{ Си-текст %} %token Список имен лексем %% Список правил трансляции %% Служебные Си-подпрограммы
Си-текст (который вместе с окружающими скобками %{ и %} может отсутствовать) обычно содержит Си-объявления (включая #include и #define), используемые в тексте ниже. Этот Си-текст может содержать и объявления (или предобъявления) функций.
Список имен лексем содержит имена, которые преобразуются YACC-препроцессором в объявления констант (#define). Как правило, эти имена используются как имена классов лексем и служат для определения интерфейса с лексическим анализатором.
Каждое правило трансляции имеет вид
Левая"часть : альтернатива"1 {семантические"действия"1} | альтернатива"2 {семантические"действия"2} |... | альтернатива"n {семантические"действия"n} ;
Каждое семантическое действие - это последовательность операторов Си. При этом каждому нетерминалу может быть сопоставлен один синтезируемый атрибут. На атрибут нетерминала левой части ссылка осуществляется посредством значка $$, на атрибуты символов правой части - посредством значков $1, $2 , . . . , $n, причем номер соответствует порядку элементов правой части, включая семантические действия. Каждое семантическое действие может вырабатывать значение в результате выполнения присваивания $$=Выражение. Исполнение текого оператора в последнем семантическом действии определяет значение атрибута символа левой части.
В некоторых случаях допускается использование грамматик, имеющих конфликты. При этом синтаксический анализатор разрешает конфликты следующим образом:
конфликты типа свертка/свертка разрешаются выбором правила, предшествующего во входной метапрограмме;конфликты типа сдвиг/свертка разрешаются предпочтением сдвига. Поскольку этих правил не всегда достаточно для правильного определения анализатора, допускается определение старшинства и ассоциативности терминалов.
Например, объявление
%left '+' '-'
определяет + и -, имеющими одинаковый приоритет и имеющими левую ассоциативность. Операцию можно определить как правоассоциативную в результате объявления:
%right '^'
Бинарную операцию можно определить как неассоциативную (то есть не допускающую появления объединения двух подряд идущих знаков операции):
%nonassoc '<'
Символы, перечисленные в одном объявлении, имеют одинаковое старшинство. Старшинство выше для каждого последующего объявления. Конфликты разрешаются путем присваивания старшинства и ассоциативности каждому правилу грамматики и каждому терминалу, участвующим в конфликте. Если необходимо выбрать между сдвигом входного символа s и сверткой по правилу A

Обычно за старшинство правила принимается старшинство самого правого терминала правила. В тех случаях, когда самый правый терминал не дает нужного приоритета, этот приоритет можно назначить следующим объявлением:
%prec терминал
Старшинство и ассоциативность правила в этом случае будут такими же, как у указанного терминала.
YACC не сообщает о конфликтах, разрешаемых с помощью ассоциативности и приоритетов. Восстановление после ошибок управляется пользователем с помощью введения в грамматику "правил ошибки" вида
A

Здесь error - ключевое слово YACC. Когда встречается синтаксическая ошибка, анализатор трактует состояние, набор ситуаций для которого содержит правило для error, некоторым специальным образом: символы из стека выталкиваются до тех пор, пока на верхушке стека не будет обнаружено состояние, для которого набор ситуаций содержит ситуацию вида [A

Если w пусто, делается свертка. После этого анализатор пропускает входные символы, пока не найдет такой, с которым можно продолжить нормальный разбор.
Если w не пусто, просматривается входная строка и делается попытка свернуть w. Если w состоит только из терминалов, эта строка ищется во входном потоке.
Системы автоматизации построения трансляторов
Системы автоматизации построения трансляторов (САПТ) предназначены для автоматизации процесса разработки трансляторов. Очевидно, что для того, чтобы описать транслятор, необходимо иметь формализм для описания. Этот формализм затем реализуется в виде входного языка САПТ. Как правило, формализмы основаны на атрибутных грамматиках. Ниже описаны две САПТ, получившие распространение: СУПЕР [4] и Yacc. В основу первой системы положены LL(1)-грамматики и L-атрибутные вычислители, в основу второй - LALR(1)-грамматики и S-атрибутные вычислители.
Формальные свойства
Придадим теперь идее использования синтезированных и унаследованных атрибутов более точную и более общую форму.
Пусть имеется КС-грамматика G = (V, N, S, P), где V - (конечный) алфавит терминальных и нетерминальных символов;


Семантические правила дополняют G следующим образом. С каждым символом X

Пусть P состоит из m правил, и пусть p-е правило имеет вид
Xp0

Пример 2.1.
(html, txt)
где np > 0, Xp0


























Грамматика (таблица 1.1), например, представляется в виде G = ({0, 1, ".", B, L, N}, {B, L, N}, N, {B






Атрибутами здесь являются
A0(B) = {v}, A1(B) = {s}; A0(L) = {v, l}, A1(L) = {s}; A0(N) = {v}, A1(N) =

и A0(x) = A1(x) =

для x

Типичным примером правил вывода служит четвeртое правило X40

t(4, 0, v) = 2,


Семантические правила используются для сопоставления цепочкам КС языка"значения" следующим образом1)
. Для любого вывода терминальной цепочки t из S при помощи синтаксических правил построим обычное дерево вывода. А именно, корнем дерева будет S, а каждый узел помечается либо терминальным символом, либо нетерминалом Xp0, соответствующим применению p-го правила для некоторого p; в последнем случае у этого узла будет np непосредственных потомков.

Рис. 2.2.
Пусть теперь X - метка некоторого узла дерева и пусть R






fpj





все атрибуты



Естественно потребовать, чтобы семантические правила давали возможность вычислить все атрибуты произвольного узла в любом дереве вывода. Если это условие выполняется, будем говорить, что семантические правила заданы корректно2)
. Поскольку деревьев вывода, вообще говоря, бесконечно много, важно уметь определять по самой грамматике, являются ли корректными еe семантические правила.
Отметим, что этот метод определения семантики обладает такой же мощностью, как и всякий другой возможный метод, в том смысле, что значение любого атрибута в любом узле может произвольным образом зависеть от структуры всего дерева. Предположим, например, что в КС грамматике всем символам, кроме S, приписано по два унаследованных атрибута: l ("положение") и t ("дерево"), а всем нетерминалам, кроме того, по одному синтезированному атрибуту s ("поддерево"). Значениями l будут конечные последовательности положительных целых чисел

 | (2.4) |

Следовательно, для дерева (рис. 1.2), например, мы имеем
s(N) = {(1, L), (2, ?), (3, L), (1.1, L), (1.2, B), (3.1, L), (3.2, B), (1.1.1, L), (1.1.2, B), (1.2.1, 1), (3.1.1, B), (3.2.1, 1), (1.1.1.1, L), (1.1.1.2, B), (1.1.2.1, 0), (3.1.1.1, 0), (1.1.1.1.1, B), (1.1.1.2.1, 1), (1.1.1.1.2.1, 1)}.
Ясно, что эта запись содержит всю информацию о дереве вывода. Согласно семантическим правилам (2.4), атрибут t во всех узлах (кроме корня) представляет собой множество, характеризующее всe дерево вывода; атрибут l определяет местонахождение этих узлов. Отсюда сразу следует, что любая мыслимая функция, определ_нная на дереве вывода, может быть представлена как атрибут произвольного узла, поскольку эта функция имеет вид f(t, l), для некоторого f. Аналогично, можно показать, что для определения значения, связанного с произвольным деревом вывода, достаточно только синтезированных атрибутов, поскольку синтезированный атрибут w, вычисляемый по формуле
 | (2.5) |
в корне дерева полностью определяет всe дерево3)
. Каждое семантическое правило, определяемое методами этого раздела, можно рассматривать как функцию этого атрибута w. Следовательно, описанный общий метод по существу не более мощен, чем метод, вовсе не использующий наследованных атрибутов. Правда, это утверждение не следует понимать как практическую рекомендацию, поскольку семантические правила, не использующие унаследованных атрибутов, будут зачастую гораздо более сложными (а также менее понимаемыми и практичными), чем правила, включающие атрибуты обоих типов. Если допустить, чтобы атрибуты в каждом узле дерева могли зависеть от всего дерева, то семантические правила часто могут стать проще и будут лучше соответствовать нашему пониманию процесса вычисления.
Обсуждение
Идея определения семантики с помощью синтезированных атрибутов, связанных с каждым нетерминальным символом и семантических правил, сопоставленных каждому правилу вывода, принадлежит Айронсу [6, 7]. Первоначально каждый нетерминальный символ имел ровно один атрибут, называвшийся его "трансляцией" . Эта идея использовалась Айронсом и позже другими авторами, особенно Маклюром [14] при построении "синтаксически управляемых компиляторов" , переводивших языки программирования в машинный код.
Как мы видели в разд. 2, синтезированных атрибутов достаточно (в принципе) для определения любой функции на дереве вывода. Но на практике применение наряду с синтезированными и унаследованных атрибутов, как описано в данной статье, приводит к значительным упрощениям. Определение Тьюрингола, например, показывает, что легко учитывается согласованность описаний и использований символов, а также между метками и операторами. Другой общей особенностью языков программирования, определение которой значительно упрощается в результате применения унаследованных атрибутов, является "блочная структура" . Вообще говоря, унаследованные атрибуты полезны всякий раз, когда часть значений некоторой конструкции определяется контекстом, в котором находится эта конструкция. Метод, приведeнный а разд. 2, показывает, как можно формально описывать унаследованные и синтезированные атрибуты, а в разд. 3 показано, что можно не принимать во внимание проблему зацикленности (являющуюся потенциальным источником трудностей при использовании атрибутов разных типов).
Автору к настоящему времени известно несколько работ, внесших принципиальный вклад в решение задачи формального описания семантики языков программирования. Это определение Алгола 60 средствами расширенного алгоритма Маркова, данное Дебаккером [1], определение Алгола 60 с помощью ?-исчисления, принадлежащее Ландину [9, 10, 11] (см. также Бeм [2, 3], определение Микро-Алгола с помощью рекурсивных функций, применяемых к программе и к _векторам состоянийї, принадлежащее Маккарти [12] (см.
также Маккарти и Пэинтер [13]; определение языка Эйлер средствами семантических правил, применяемых во время синтаксического анализа программы, предложенное Виртом и Вебером [16], и определение языка PL=I, данное Венской лабораторией фирмы IBM и основанное на работе Маккарти и Ландина, а также на понятии абстрактной машины, введ_нном Элготом [4, 5]. Наиболее существенная разница между предшествующими методами и описанием языка Тьюрингол, привед_нным в таблица 1, состоит в том, что остальные
определения представляют собой довольно сложные процессы, применяемые ко всей программе; можно сказать, что человек, прежде чем он поймeт описание языка, должен будет понять, как устроен его компилятор. Эта трудность особенно ощутима в работе Дебаккера, определяющего машину, подобную Марковским алгоритмам, но значительно более сложную. Эта машина имеет около 800 команд. На каждом шаге вычисления машины нужно выполнять последнюю применимую команду, так что мы не можем проверить, нужно ли выполнить команду номер 100, до тех пор, пока не убедимся, что остальные 700 команд неприменимы. Кроме того, в процессе работы машины список пополняется новыми командами. Ясно, что читателю чрезвычайно трудно понять работу такой машины или формально доказать ee основные свойства. Описание Тьюрингола, напротив, определяет каждую конструкцию языка только через еe "непосредственное окружение" , сводя тем самым к минимуму взаимосвязи между определениями разных частей языка. Определение составных операторов, операторов перехода и т.д. не влияет существенно на определение оператора печати; например, любое из правил 4.1, 4.2, 4.3, 4.4, 5.1, 5.3 можно выбросить, и получится строгое определение другого языка. Такая локализация и разделение семантических
правил помогает сделать определение более понятным и кратким. Хотя определения остальных авторов, упомянутые выше, не так сложны, как определение Дебаккера, в их работах всe-таки присутствуют относительно сложные зависимости между отдельными частями определения.
Рассмотрим, например, формальное определение языка Эйлер, данное Виртом и Вебером [16]. Это краткое описание весьма сложного языка и потому, безусловно, оно является одним из наиболее удачных формальных определений. И всe же, несмотря на то, что Вирт и Вебер проверили своe определение с помощью моделирования на вычислительной машине, весьма вероятно, что некоторые черты Эйлера удивят его создателей. Следующая программа на Эйлере синтаксически и семантически правильна, хотя после метки L нигде не встречаются двоеточия:

Результатом работы этой программы будет 1, 2, 2, 3! Промахи такого рода не являются неожиданностью при алгоритмическом определении языка. При использовании методов разд. 4 подобные ошибки менее вероятны.
Есть основания утверждать, что ни одна из предыдущих схем (формального определения семантики) не в состоянии дать такого же краткого и простого для понимания определения Тьюрингола, как то, которое представлено выше. Кроме того (хотя детали окончательно не проработаны), оказывается, что Алгол 60, Эйлер, Микро- Алгол и PL=1 также можно определить методами разд. 4, причeм все преимущества по сравнению с остальными методами сохраняются. Правда, здесь автор не может быть беспристрастным судьeй, поэтому для подтверждения такой точки зрения требуется некоторый дополнительный опыт.
Отметим, что семантические правила в том виде, в котором они даны в настоящей статье, не зависят от конкретно выбранного метода синтаксического анализа. На самом деле они привязаны даже к конкретным формам синтаксиса. Единственное от чего зависят семантические правила - это имя нетерминала в левой части синтаксического правила и имени нетерминалов в правой его части. Конкретные знаки пунктуации и порядок, в котором нетерминалы располагаются в правых частях правил, несущественны с точки зрения семантических правил. Таким образом, рассматриваемое здесь определение семантики хорошо сочетается с идеей Маккарти об "абстрактном синтаксисе" [12, 13].
Когда синтаксис неоднозначен в том смысле, что некоторые цепочки языка имеют более одного дерева вывода, семантические правила дают для каждого дерева вывода своe "значение" .
Предположим, например, что к грамматике (1.3) добавлены правила

Грамматика в результате становится синтаксически неоднозначной, но остаeтся по-прежнему семантически однозначной, поскольку атрибут v(N) имеет одно и то же значение для всех деревьев вывода. С другой стороны, если изменить правило 5.2 определения Тьюрингола с S


Простой язык программирования
Сейчас мы продемонстрируем, как описанный выше метод семантического определения можно применять к языкам программирования. Для простоты изучим формальное определение небольшого языка, описывающего программы для машин Тьюринга.
Машина Тьюринга (в классическом смысле) работает с бесконечной лентой, которую можно представлять себе раздел_нной на клетки. Машина может считывать или записывать символы некоторого конечного алфавита в обозреваемую в некоторый момент клетку, а также сдвигать читающее устройство на одну клетку вправо или влево. Следующая программа, например, прибавляет единицу к целому числу, представленному в двоичном виде, и печатает точку справа от этого числа. Предполагается, что в начале и в конце работы программы читающее устройство находится на первой пустой клетке справа от числа.
Алфавит пробел, единица, нуль, точка; печатать "точка"; перейти на выполнить; тест: если символ на ленте _единицаї, то {печатать "нуль"; (4.1) выполнить: сдвинуться влево на одну клетку; перейти на тест}; печатать "единица"; возврат: сдвинуться вправо на одну клетку; если символ на ленте "нуль", то перейти на возврат.
Читатель, по-видимому, найдeт этот язык программирования достаточно прозрачным для того, чтобы понять его, прежде чем будет дано какое-либо формальное определение, хотя это и не обязательно. Приведeнная выше программа не является примером искусного программирования. Она лишь иллюстрирует некоторые черты простого языка, рассматриваемого в настоящем разделе.
Поскольку каждый язык программирования нужно как- то называть, назовeм наш язык Тьюринголом. Всякая правильная программа на Тьюринголе определяет программу для машины Тьюринга; будем говорить, что программа для машины Тьюринга состоит из:
множества "состояний" Q,множества "символов" ?начального "состояния" q0



(Q-{q?})x? в ?{-1, 0, +1}xQ. Если

Формально программа машины Тьюринга определяет вычисление для ленты с "любым начальным содержимым", то есть для любой бесконечной в обе стороны последовательности
...,a-3, a-2, a-1, a0, a1, a2, a3,...
Пример 4.2.
(html, txt)
элементов алфавита ? следующим образом. В произвольный момент вычисления существует "текущее состояние" q



Теперь, когда у нас имеется точное определение программ машин Тьюринга, мы хотим определить программу машины Тьюринга, соответствующую произвольной программе на Тьюринголе (и одновременно определить синтаксис Тьюрингола). Для этого удобно принять некоторое соглашение о форме записи.
(1) Семантическое правило " включить х в B ", связанное с синтаксическим правилом, означает, что x должен стать элементом множества B, где B - атрибут аксиомы S грамматики. Значением B будет множество всех x, для которых существует такое семантическое правило, связанное с каждым применением соответствующего синтаксического правила в дереве вывода. (Это правило можно рассматривать как сокращeнную запись семантического правила

связанного с каждым синтаксическим правилом. Здесь B - синтезированный атрибут, имеющийся у всех нетерминальных символов. Для терминальных символов B(x) пусто. Ясно, что эти правила позволяют получить нужное B(S).)
(2) Семантическое правило "определить f(x) = y", связанное с синтаксическим правилом, означает, что значение функции f в точке x будет равно y; здесь f - атрибут аксиомы S грамматики. Если встречается два правила, задающих значение f(x) для одного и того же значения x, то возникает ситуация ошибки, а дерево вывода, в котором она возникла, называется неправильным.
Далее, к функции f можно обращаться в других семантических правилах при условии, что f(x) будет использоваться только тогда, когда значение функции для аргумента x определено. Любое дерево вывода, для которого
встретилось обращение к неопределeнной величине f(x), называется неправильным. (Правила такого типа важны, например, тогда, когда нужно обеспечить соответствие между описанием и использованием идентификаторов. В приведeнном ниже примере в соответствии с этим соглашением неправильными будут программы, в которых один и тот же идентификатор дважды встречается в качестве метки, или в операторе перехода используется идентификатор, не являющийся меткой оператора. В сущности, это правило можно представлять себе, аналогично (1), как " включить (x, y) в f", если рассматривать f как множество упорядоченных пар; необходимо соответственно ввести дополнительные проверки на зацикленность. Признак "правильно или неправильно" можно считать атрибутом аксиомы S. Построение соответствующих семантических правил, аналогичных (4.3), которые аккуратно определяют запись "определить f(x) = y", несложно и предоставляется читателю.)
(3) Функция "новсимвол", в каком бы правиле она ни встретилась, будет вырабатывать некий абстрактный объект, причeм при каждом обращении к "новсимвол" этот объект будет отличен от всех полученных при предшествовавших обращениях к новсимвол. (Эту функцию легко выразить при помощи других семантических правил, например используя атрибуты l из (2.3), принимающие в разных вершинах дерева разные значения. Функция новсимвол служит подходящим источником "сырья" для построения множеств.)
Мы видели, что соглашения (1), (2) и (3) можно заменить другими семантическими конструкциями, не использующими таких соглашений, следовательно, они не являются "базисными" для семантики. Но они чрезвычайно полезны, так как соответствуют понятиям, которыми часто пользуются, поэтому их можно считать принципиальными для метода описания семантики, представленного в настоящей статье.
Эффект от введения таких соглашений состоит в том, что уменьшается общее количество атрибутов, явно присутствующих в правилах, и в том, что удаeтся обойтись без неоправданно длинных правил. Теперь уже несложно дать формальное определение синтаксиса и семантики Тьюрингола.
Нетерминальные символы:
P (программа), S (оператор), L (список операторов), I (идентификатор), O (направление), A (символ алфавита), D (описание).
Терминальные символы:
a b c d e f g h i j k l m n o p q r s t u v w x y z . , : ; ' ' { }
алфавит перейти на печатать если символ на ленте то сдвинуться на одну клетку влево вправо
Начальный символ: p
Атрибуты:
| Имя атрибута | Тип значения | Цель введения |
| Q | Множество | Состояния программы |
| ? | Множество | Символы программы |
| q0 | Элемент множества Q | Начальное состояние |
| q? | Элемент множества Q | Конечное состояние |
 | Функция, отображающая (Q - {q?}) x ? в ? x {-1, 0, +1} x Q | Функция переходов |
| метка | Функция, отображающая цепочки букв в элементы мн-ва Q | Таблица состояний для операторных меток |
| символ | Функция, отображающая цепочки букв в элементы множества ? | Таблица символов для символов ленты |
| следующее | Элемент множества Q | Состояние,непосредственно следующее за оператором или списком операторов |
| d | ±1 | Направление |
| текст | Цепочка букв | Идентификатор |
| Содержание | Элемент множества Q | Состояние в начале выполнения оператора или списка операторов (унаследованный атрибут) |
Синтаксические и семантические правила см. в таблица 1.
| Комментарий | № | Синтаксическое правило | Пример | Семантическое правило |
| Буквы | 1.1 ... 1.26 | A   | a ...(так же z | текст (A) = a для всех букв) текст (A) = z |
| Идентификаторы | 2.1 2.2 | I   | m marilyn | текст (I) = текст (A) текст (I) = текст(I) текст |
| Описания | 3.1 | D | алфавит marilyn | определить символ (текст (I)) = новсимвол; включить символ (текст (I)) в ? |
| Описания | 3.2 | D | алфавит marilyn, jayne, brigitta | определить символ (текст (I)) = новсимвол; включить символ (текст (I)) в ? |
| Оператор печати | 4.1 | S | печатать "jayne" | определить   следующий (S) в Q. |
| Оператор сдвига | 4.2 | S | сдвинуться влево на одну клетку | определить   |
| 4.2.1 | О | влево | d(O) = -1. | |
| 4.2.2 | О вправо | вправо | d(O) = +1. | |
| Оператор перехода | 4.3 | S  | перейти на boston | определить   следующий (S) в Q. |
| Пустой оператор | 4.4 | S  | следующий (S) = начало (S) | |
| Условный оператор | 5.1 | S1  | еслисимвол на ленте marilyn , то печатать jayne | определить    |
| Помеченный оператор | 5.2 | S1 | boston: сдвинуться влево на одну клетку | определить метка (текст (I))= начало (S1): начало (S2)=начало (S1); следующий (S1)= следующий (S2) |
| Составной оператор | 5.3 | S  | (печатать "jayne" перейти на boston | начало (L)=начало (S); следующий (S) = следующий (L). |
| Список опера- торов | 6.1 | L  | печатать "jayne" | начало (L)=начало (S); следующий (L) = следующий (S). |
| 6.2 | L1 | печатать "jayne" перейти на boston | начало (L2)=начало (L1); начало (S) = следующий (L2). следующий (L1) = следующий (S). | |
| Программа | 7 | Р  | алфавит marilyn, jayne, birgitta печатать "jayne" | q=новсимвол; включить q0 в Q; начало (L)=q0; q?= следующий (L). |
/p> Отметим, что каждому оператору S соответствует два состояния: начало (S) - состояние, соответствующее первой команде, входящей в оператор (если таковая имеется), являющееся унаследованным атрибутом символа S, и следующее (S) - состояние, "следующее" за оператором, или состояние, в которое попадает машина после нормального выполнения оператора. В случае оператора перехода, однако, программа не попадeт в состояние следующее (S), поскольку действие оператора состоит в передаче управления в другое место; о состоянии следующее (S) можно сказать, что оно следует за оператором "статически" или "текстуально" , а не "динамически" в ходе выполнения программы.
В таблица 1 следующее (S) является синтезированным атрибутом; можно составить аналогичные семантические правила, в которых атрибут следующее (S) будет унаследованным. При этом, правда, программы, включающие пустые операторы, будут несколько менее эффективны (см. правило 4.4). Аналогично, оба атрибута начало (S) и следующее (S) могут быть сделаны синтезированными, но это будет стоить дополнительных инструкций в программе машины Тьюринга при реализации списка операторов.
Наш пример мог бы быть проще, если бы мы использовали менее традиционную форму инструкций машины Тьюринга. Принятое нами определение требует, чтобы каждая инструкция включала действия чтения, печати и сдвига читающего устройства. Машина Тьюринга представляется при этом в виде некоей одно-плюс-одно- адресной вычислительной машины, в которой каждая инструкция определяет местоположение (состояние) следующей инструкции. Метод определения семантических правил, использованный в этом примере, где атрибут следующее (S) является синтезированным, а начало (S) - унаследованным, годится и для вычислительной машины или автомата, в котором n + 1-я инструкция выполняется после n-й. В этом случае (следующее (S) - начало (S)) есть число инструкций, "скомпилированных" для оператора S.
Создаeтся впечатление, что такое определение Тьюрингола приближает нас к желанной цели: придать точный смысл тем понятиям, которые встречаются в неформальном руководстве по языку для программиста, причeм сделать это нужно совершенно формально и однозначно.Другими словами, это определение, возможно, отвечает нашему образу мышления при изучении языка. Определение 4.1 оператора печати, например, можно легко перевести на естественный язык, написав
Оператор может иметь вид: печатать "I"
где I - идентификатор. Это означает, что всякий раз при выполнении этого оператора символ на обозреваемой клетке ленты будет заменeн символом, обозначенным I, безотносительно к тому, какой символ находится в обозреваемой клетке. После этого выполнение программы продолжится с новой инструкции, которая определяется (другими правилами) как следующая за данным оператором
Проверка на зацикленность
Рассмотрим теперь алгоритм, проверяющий, является ли корректной система семантических правил, определeнная в предыдущем разделе. Другими словами, мы хотим знать, когда семантические правила позволяют вычислить значение любого атрибута любого узла произвольного дерева вывода. Можно считать, что грамматика не содержит "бесполезных" правил вывода, то есть что каждое правило из P участвует в выводе хотя бы одной терминальной цепочки.
Пусть T - произвольное дерево вывода, соответствующее данной грамматике; метками концевых узлов могут быть только терминальные символы, корню же разрешим иметь меткой не только аксиому, но и любой символ из V . Тогда можно определить ориентированный граф D(T), соответствующий T, взяв в качестве его узлов упорядоченные пары (X,







Рис. 3.1.
Другими словами, узлами графа D(T) служат атрибуты, значения которых нужно вычислить, а дуги определяют зависимости, подразумевающие, какие атрибуты вычисляются раньше, а какие позже (рис. 1.6).
Ясно, что семантические правила являются корректными тогда и только тогда, когда ни один из орграфов D(T) не содержит ориентированного цикла. Дело в том, что если в графе нет ориентированных циклов, то можно применить хорошо известную процедуру, позволяющую присвоить значения всем атрибутам. Если же в некотором графе D(T) есть ориентированный цикл, то ввиду того что грамматика не содержит бесполезных правил, можно утверждать, что существует ориентированный цикл в некотором графе D(T), у которого меткой корня дерева T служит S. Для такого дерева T все атрибуты вычислить не уда_тся. Таким образом, задача "Являются ли семантические правила корректным?" сводится к задаче "Содержат ли орграфы D(T) ориентированные циклы?"
Каждый орграф D(T) можно рассматривать как суперпозицию меньших орграфов Dp, соответствующих правилам Xp0
























Рис. 3.2.
Орграф (рис. 3.1) получается в результате "объединения" таких подграфов. Вообще, если T имеет в качестве метки корня терминал, D(T) не содержит дуг. Если корень дерева T помечен нетерминальным символом, T имеет вид

Рис. 3.3.
для некоторого p, где Tj - дерево вывода, у которого корень помечен символом Xpj, где 1




Для проверки того, содержит ли граф D(T) ориентированный цикл, нам понадобится ещe одно понятие. Пусть p - номер правила вывода. Обозначим через Gj
произвольный орграф (1


Dp[G1,..., Gnp ]
Пример 3.4.
(html, txt)
орграф, полученный из Dp добавлением дуг, идущих из (Xpj,




Например, если

и если D4 - ориентированный граф из (3.2), то D4(G1, G2) имеет вид

Рис. 3.4.
Теперь можно воспользоваться следующим алгоритмом. Для любого X



Будем добавлять к множествам S(X) новые орграфы при помощи следующей процедуры до тех пор, пока в S(X) не перестанут появляться новые элементы. Выберем целое p; 1







 | (3.5) |
существует ориентированный путь из (Xp0;


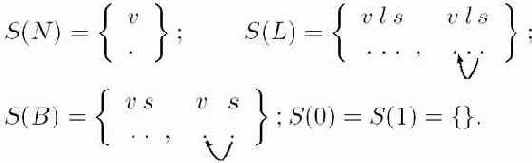
Пусть T - дерево вывода с корнем X, и пусть D'(T) - ориентированный граф с множеством узлов A(X), у которого есть дуга из





. Действительно, построение не добавляет к S(X) новых ориентированных графов, не являющихся D'(T). Алгоритм можно даже легко обобщить так, чтобы для каждого графа из S(X) он печатал на выходе соответствующее дерево вывода T. Обратно, если T - дерево вывода, мы можем показать индукцией по числу узлов дерева T, что D'(T) принадлежит некоторому множеству S(X). В противном случае T должно иметь вид (3.3) и D(T) "составлен" из






Вышеприведeнный алгоритм решает задачу, поставленную в этом разделе.
Теорема. Семантические правила, добавленные к грамматике так, как это сделано в разд. 2, являются корректными тогда и только тогда, когда ни один из ориентированных графов (3.5) ни при каком выборе p и

Доказательство. Если (3.5) содержит ориентированный цикл, то, как было показано выше, некоторый D(T) содержит ориентированный цикл. Наоборот, если T - дерево с наименьшим возможным числом улов, такое, что D(T) содержит ориентированный цикл, то T должно иметь вид (рис. 3.3), а D(T) "составляется" из


что нам нужно дать точное
Допустим, что нам нужно дать точное определение двоичной системы записи чисел. Это можно сделать многими способами. В данном разделе мы рассмотрим метод, который может быть использован и для других систем счисления. В случае двоичной системы этот метод сводится к определению, основанному на следующей констекстно-свободной (КС) грамматике.
B






Пример 1.1.
(html, txt)
Здесь терминальными символами являются ".", "0" и "1", нетерминальными - B, L и N, обозначающие соответственно бит, список битов и число. Двоичным числом будем считать любую цепочку терминальных символов, выводимую из N при помощи правил (пример 1.1). Эта грамматика в действительности выражает тот факт, что двоичное число представляет собой последовательность из одного или более нулей и единиц, за которой может следовать точка и еще одна последовательность нулей и единиц. Кроме того, грамматика приписывает каждому двоичному числу определенную древовидную структуру. Например, цепочка 1101.01 получает следующую структуру:

Рис. 1.2.
Естественно определять значение двоичной записи (пример 1.1) с помощью некоторого пошагового процесса, сопоставленного ее структуре (рис. 1.2); значение всей двоичной записи строится из значений отдельных частей. Это можно сделать, приписав каждому нетерминалу атрибуты следующим образом:




(Заметим, что у всех нетерминалов L по два атрибута; вообще говоря, каждому нетерминалу можно приписывать любое желаемое число атрибутов).
Грамматику (пример 1.1) можно теперь расширить так, чтобы каждому синтаксическому правилу отвечали семантические правила.
B






Пример 1.3.
(html, txt)
(Индексы в четвертом и шестом правилах применяются для того, чтобы различать вхождения одноименных нетерминалов.). В этих семантических правилах значения атрибутов всех нетерминалов определяются через значения атрибутов их непосредственных потомков, так что окончательные значения определены для всех атрибутов. Предполагается, что смысл обозначений, использованных для записи семантических правил, понятен. Отметим, например, что символ "0" в семантическом правиле v(B) = 0 понимается не так, как символ "0" в синтаксическом правиле B

Структуру (рис. 1.2) можно расширить, выписав явно атрибуты при всех узлах.

Рис. 1.4.
Таким образом, "1101.01" обозначает 13.25 (в десятичной записи).
Такой способ определения семантики КС-языков в сущности хорошо известен, так как он уже использовался несколькими авторами. Однако существует важное расширение этого метода. Именно это расширение и представляет для нас интерес.
Предположим, например, что мы хотим определить семантику двоичной записи другим способом, более близким к нашему обычному ее пониманию. Первая единица в записи 1101.01 на самом деле означает 8, хотя в соответствии с (рис. 1.4) ей приписывается значение 1. Возможно, поэтому будет лучше определять семантику таким образом, чтобы местоположение символа тоже играло определ_нную роль. Можно ввести следующие атрибуты:






Эти атрибуты можно определить следующим образом:
| Синтаксические правила | Семантические правила |
B  | v(B) = 0 |
B  | v(B) = 2s(B) |
L  | v(L) = v(B), s(B) = s(L), l(L) = 1 |
L1  | v(L1) = v(L2) + v(B), s(B) = s(L1), s(L2) = s(L1) + 1, l(L1) = l(L2) + 1 |
N  | v(N) = v(L); s(L) = 0 |
N  | v(N) = v(L1) + v(L2), s(L1) = 0, s(L2) = -l(L2) |
Здесь при записи семантических правил принято следующее соглашение. Правая часть каждого правила представляет собой определение левой части, таким образом, s(B) = s(L) означает, что сначала должно быть вычислено s(L), а затем полученное значение следует присвоить s(B).
Важным свойством грамматики (таблица 1.1) является то, что некоторые из атрибутов, которым присваиваются значения, приписаны нетерминалам, стоящим в правой части соответствующего синтаксического правила, в то время как в 1.3 атрибуты левых частей семантических правил относились только к нетерминалам, стоящим в левой части синтаксического правила. Здесь мы используем как синтезированные атрибуты (вычисляемые через атрибуты потомков данного нетерминала), так и унаследованные атрибуты (вычисляемые через атрибуты предков). Синтезированные атрибуты вычисляются в древовидной структуре снизу вверх, а унаследованные - сверху вниз. Грамматика (таблица 1.1) включает синтезированные атрибуты v(B), v(L), l(L), v(N) и унаследованные атрибуты s(B) и s(L), так что при их вычислении необходимо проходить по дереву в обоих направлениях. Вычисление на структуре, соответствующей цепочке 1101.01, имеет вид:

Рис. 1.6.
Можно заметить, что атрибуты "длина" символов L, стоящих справа от точки, должны быть вычислены снизу вверх до того, как будут вычислены (сверху вниз) атрибуты "масштаб" и атрибуты "значение" (снизу вверх).
Грамматика (таблица 1.1), вероятно, не является "наилучшей возможной" грамматикой для системы двоичной записи, но похоже, что она лучше согласуется с нашей интуицией, чем грамматика (пример 1.3). (Грамматика, которая более точно соответствует нашему традиционному толкованию двоичной нотации, содержит другое множество правил вывода.
Эти правила сопоставляют цепочке битов справа от точки иную структуру, вследствие чего атрибут "длина", не играющий принципиальной роли, становится ненужным.)
Наш интерес к грамматике (таблица 1.1) вызван не тем, что она представляет собой идеальное определение двоичной системы записи, а тем, что она демонстрирует взаимодействие унаследованных и синтезированных атрибутов. Тот факт, что семантические правила, подобные правилам в (таблица 1.1), не приводят к зацикленности определения атрибутов, не является очевидным, поскольку здесь атрибуты вычисляются не при однократном обходе дерева в одном направлении. Алгоритм, проверяющий семантические правила на зацикленность, будет описан ниже.
Важность унаследованных атрибутов состоит в том, что они естественно возникают в практике и в очевидном смысле "двойственны" синтезированным атрибутам. Хотя для определения смысла двоичной записи достаточно только синтезированных атрибутов, существует ряд языков, для которых такое ограничение приводит к неуклюжему и неестественному определению семантики. Ситуации, когда встречаются и унаследованные, и синтезированные атрибуты, представляют собой те самые случаи, которые в предшествующих определениях семантики вызывали серьезные трудности.
Абсолютно незацикленные атрибутные грамматики
Обозначим IOx ориентированный граф, вершинами которого являются атрибуты символа X и из вершины b идет дуга в вершину a тогда и только тогда, когда в атрибутной грамматике AG существует такое поддерево с корнем X, что в графе зависимостей этого поддерева существует путь из b в a. Через

Атрибутная грамматика называется абсолютно незацикленной (ANC), если ни один из графов D не содержит ориентированных циклов [6].
Абсолютно незацикленные атрибутные грамматики образуют собственный подкласс незацикленных атрибутных грамматик.
Пример B.1. Незацикленная атрибутная грамматика, не являющаяся абсолютно незацикленной (рис. B.1.).

Рис. B.1.
Эта грамматика порождает всего два слова b и bb. Каждое из двух деревьев порождает незацикленные графы зависимостей, однако грамматика не является абсолютно незацикленной. Происходит это от того, что зависимости, реализуемые в разных деревьях, "накладываются" на один граф IO.
Для построения графов IO имеется простой полиномиальный алгоритм:
Алгоритм B.3. Построение графов IO атрибутной грамматики AG.

Поскольку этот алгоритм полиномиален и задача определения наличия ориентированных циклов в графе также полиномиальна, справедлива следующая теорема:
Теорема B.9. Задача определения, является ли данная атрибутная грамматика абсолютно незацикленной, полиномиальна по длине атрибутной грамматики. Абсолютно незацикленные атрибутные грамматики интересны тем, что для них имеется полиномиальный алгоритм планирования визитов.
Обозначим через A(p) множество атрибутов символов синтаксического правила p. Рассмотрим атрибутированное дерево t в AG и некоторую его внутреннюю вершину n, в которой применено правило вывода p. В каждый момент времени в процессе вычисления атрибутов дерева t каким- либо алгоритмом вычисления какие-то атрибуты из A(p) вычислены, а какие-то нет. Назовем состоянием правила, примененного в дереве вывода, множество вычисленных атрибутов символов, входящих в это правило.
Начальным состоянием для каждого правила является множество {a<k> j Xk

План - это последовательность инструкций вида fpa<k> или V ISIT (k, I), где


Обозначим Dpa<k> - множество аргументов семантического правила fpa<k>. Будем говорить, что семантическое правило f готово к вычислению в состоянии A правила p, если a<k>


Если p : X0





Планирование осуществляется нижеследующим алгоритмом. Результат работы алгоритма заносится в двумерный массив EVAL, одним входом в который служит состояние правила, другим - входное множество. Строка - это строка инструкций Stv - вектор состояний правил; он передается как аргумент процедуре PLAN, затем дублируется внутри процедуры PLAN и обращение к PLAN меняет значение своего аргумента в точке вызова (что обозначено знаком var перед параметром Stv процедуры PLAN). Если для некоторого элемента таблицы EVAL в процедуре PLAN начато построение плана, то этот элемент метится значком @, чтобы избежать бесконечной рекурсии. Будем говорить, что функция f готова к вычислению, если все еe аргументы определены, но атрибут, который она вычисляет не определeн.
Алгоритм B.4. Построение планов для каждого возможного состояния каждого правила.
var EVAL : array[состояние, входное множество] of строка; St : array [1 .. P] of состояние; fP - число синтаксических правил} procedure PLAN( p, I, var Stv); {p - номер синтаксического правила, I - входное множество, Stv - вектор состояния правил} var S : строка {строящийся план}; LStv : array [1 ..
p] of состояние; {локальный вектор состояния правил} A : set of атрибут;{ состояние правила p} stop: boolean; begin if (EVAL [Stv[p], I] пуст) then A := I [ Stv[p], s := пусто , LStv := Stv; stop := false, EVAL [Stv[p], I] :='@' repeat if (





Вычисление атрибутов на дереве t заключается в выполнении построенных планов в соответствии с изменениями состояний правил и осуществляется следующей программой:
begin каждое правило дерева t перевести в начальное состояние, определяемое множеством атрибутов терминалов; V ISIT(корень, {}) end.
Атрибутированное дерево разбора
Если дана атрибутная грамматика AG и цепочка, принадлежащая языку, определяемому G, то можно построить дерево разбора этой цепочки в грамматике G. В этом дереве каждая вершина помечена символом грамматики G. Припишем теперь каждой вершине множество атрибутов, сопоставленных символу, которым помечена эта вершина. Атрибуты, сопоставленные вхождениям символов в дерево разбора, будем называть вхождениями атрибутов в дерево разбора, а дерево с сопоставленными каждой вершине атрибутами - атрибутированным деревом разбора.
Между вхождениями атрибутов в дерево разбора существуют зависимости, определяемые семантическими правилами, соответствующими примененным синтаксическим правилам.
Для каждого синтаксического правила p

a(j) = fpa(j)(... , b(i), ...), i, j

Граф зависимостей D(t) дерева разбора t цепочки, принадлежащей языку грамматики G, определим как ориентированный граф, полученный объединением графов зависимостей всех примененных в t синтаксических правил.
Чистые многовизитные грамматики
Будем говорить, что атрибутированное дерево k-визитно, если существует вычислительная последовательность cs для t такая, что никакая вершина n из t не посещается более k раз.
Атрибутная грамматика называется чистой k-визитной (PMV ), если каждое атрибутированное дерево вывода t в AG k-визитно [5, 7].
Теорема B.6. Для всякой корректной атрибутной грамматики существует k такое, что грамматика является чистой k-визитной.
На самом деле это k не превосходит максимального по всем символам грамматики числа синтезируемых или наследуемых атрибутов.
Следствием этого являются две следующие теоремы.
Теорема B.7. Сложность задачи определения того, является ли произвольная атрибутная грамматика чистой k-визитной для какого-нибудь k > 0, экспоненциальна.
Эта задача просто совпадает с задачей определения корректности атрибутной грамматики.
Теорема B.8. Сложность задачи определения того, является ли произвольная атрибутная грамматика чистой k-визитной для фиксированного k также экспоненциальна.
Атрибуты всякого дерева t чистой k-визитной атрибутной грамматики можно вычислить с помощью следующего алгоритма:
Алгоритм B.2. Вычисление атрибутов чистой k- визитной атрибутной грамматики
procedure визит_в_поддерево (n, i); {n - корень поддерева; i - номер визита в это поддерево} {Предполагается, что в вершине n применено правило вывода p} begin вычислить некоторые наследуемые атрибуты Xn; {эти атрибуты определяются <nj1, A> для начала i-го визита в соответствующей вычислительной последовательности} визит_в_поддерево (n, i); {Xnij - символ правой части правила pg . . . визит_в_поддерево (njl, ijl); вычислить некоторые синтезируемые атрибуты Xn end; begin for j := 1 to k do визит_в_поддерево(r, j) {r - корень дерева} end end.
В зависимости от того, какие ограничения будут накладываться на порядок посещения вершин и выбор атрибутов, вычисляемых на том или ином визите, будут получаться те или иные классы атрибутных грамматик.
Многопроходные грамматики
Пусть на последовательность визитов наложено такое ограничение, чтобы они образовали последовательные обходы дерева разбора либо сверху-вниз слева-направо, либо сверху- вниз справа-налево.
Атрибутная грамматика называется чистой k- проходной в обоих направлениях, если существует такая последовательность из k обходов <d1 ... dl> (каждое di - либо справа-налево, либо слева-направо), что атрибуты любого дерева вывода могут быть вычислены в результате выполнения этой последовательности обходов [5].
Атрибутная грамматика называется чистой многопроходной в обоих направлениях (PBD), если она является чистой k-проходной в обоих направлениях для какого-нибудь k.
Пример B.3. Существуют атрибутные грамматики, не являющимися чистыми многопроходными ни для какого k ( рис. B.3).

Рис. B.3.
Число необходимых проходов в этом примере зависит от глубины дерева и может быть сколь угодно большим.
Очевидно, что грамматика примера рис. B.1 не является чистой многопроходной и нетрудно видеть, что грамматика примера рис. B.1 является абсолютно незацикленной.
Теорема B.14. Задача определения того, является ли произвольная атрибутная грамматика чистой многопроходной в обоих направлениях, зависит экспоненцально от размера атрибутной грамматики.
Атрибутная грамматика называется чистой k-проходной слева-направо, если атрибуты любого дерева вывода в ней могут быть вычислены за k обходов дерева вывода слева- направо [2, 5].
Атрибутная грамматика называется чистой многопроходной слева-направо (PLR), если она является чистой k-проходной слева-направо для какого-нибудь k.
Незацикленные атрибутные грамматики
Атрибутная грамматика называется незацикленной, если графы зависимостей деревьев всех цепочек, принадлежащих языку, определяемому грамматикой G, не содержат циклов, и зацикленной, если существует хотя бы одна цепочка, принадлежащая языку, для дерева разбора которой граф D(t) содержит ориентированный цикл.
Теорема B.1. Задача определения того, является ли данная атрибутная грамматика зацикленной, имеет экспоненциальную временную сложность, то есть существует константа c > 0 такая, что любой алгоритм, проверяющий на зацикленность произвольную атрибутную грамматику размера n, должен работать более, чем 2cn/log n шагов на бесконечно большом числе грамматик [1, 2].
Кнутом [3] был предложен алгоритм проверки атрибутных грамматик на зацикленность.
Пусть D(p) - граф зависимостей атрибутов правила вывода p, а Gi - произвольный ориентированный граф, вершинами которого служат атрибуты символа Xi правой части правила вывода p. Обозначим

ориентированный граф, полученный из D(p) добавлением дуг, идущих из b(i) в a(i), если в графе Gi есть дуга из b в a. Через ?обозначим множество ориентированных графов с вершинами - атрибутами символа X, через

- ориентированный граф, вершинами которого служат атрибуты символа X в правиле вывода p : X0

и в котором идет дуга из вершины b в вершину a тогда и только тогда, когда в

Алгоритм B.1. (Алгоритм Кнута). Проверка атрибутной грамматики на зацикленность.

Теорема B.2. Атрибутная грамматика AG незациклена тогда и только тогда, когда ни один из графов Dp[G1 ... Gnp] не содержит ориентированных циклов, то есть когда алгоритм B.1. заканчивается со значением cycle = false.
Теорема B.3. Алгоритм Кнута проверки на зацикленность атрибутной грамматики размера n требует в общем случае exp(cn2) шагов.
Одновизитные атрибутные грамматики
Интересный частный случай простых многовизитных грамматик представляют одновизитные грамматики (IV)[8].
Графом BG братьев правила p будем называть граф, вершинами которого являются символы правой части правила p : X0


Теорема B.12. Атрибутная грамматика является одновизитной тогда и только тогда, когда ни один из графов братьев BGp не содержит ориентированных циклов [9].
Из этой теоремы непосредственно следует
Теорема B.13. Задача определения того, является ли произвольная атрибутная грамматика одновизитной, полиномиальна.
Задача планирования визитов для одновизитных грамматик сводится к нахождению какого-нибудь линейного порядка братьев каждого правила, удовлетворяющего частичному порядку, определяемому графом братьев BGp: Алгоритм вычисления атрибутов для одновизитных грамматик выглядит следующим образом:
Алгоритм B.6. Вычисление атрибутов в одновизитной грамматике.
procedure визит_в_поддерево (n); begin вычислить наследуемые атрибуты I(X); в соответствии с линейным порядком символов правой части правила do визит_в_поддерево (n); вычислить синтезируемые атрибуты S(X) end; begin визит_в_поддерево(r) {r - корень} end.
Пусть G - КС-грамматика: G = (T, N, P, Z), где T, N, P, Z, соответственно, множество терминальных символов, нетерминальных символов, множество правил вывода и аксиома грамматики. Правила вывода КС- грамматики будем записывать в виде
p : X0

и будем предполагать, что G - редуцированная КС- грамматика, то есть в ней нет нетерминальных символов, для которых не существует полного дерева вывода, в которое входит этот нетерминал. С каждым символом X



С каждым правилом вывода p

a0(i0) = fpa0(i0)(a1(i1), ... , aj(ij));
где ik


КС-грамматику, каждому символу которой сопоставлено множество атрибутов, а каждому правилу вывода - множество семантических правил, будем называть атрибутной грамматикой (AG).
Назовем атрибут a(X0) синтезируемым, если одному из правил вывода p : X0



Пусть правилу вывода p : X0




Простые многовизитные атрибутные грамматики
Атрибутная грамматика называется простой k-визитной, если для каждого нетерминала X



Атрибутная грамматика называется простой многовизитной (SMV ), если она является простой k-визитной для какого-нибудь k.
Существуют абсолютно незацикленные атрибутные грамматики, не являющиеся простыми многовизитными.
Пример B.2. Здесь атрибуты a и b символа A левого поддерева вычисляются на первом визите, а x и y - на втором. Для символа A правого поддерева наоборот - атрибуты x и y вычисляются на первом визите, a и b - на втором ( рис. B.2).

Рис. B.2.
Теорема B.10. Всякая простая k-визитная грамматика является абсолютно незацикленной [7].
Теорема B.11. Задача определения того, является ли произвольная атрибутная грамматика простой многовизитной, NP-полна [7]. Мало того, NP-полна даже задача определения простой 2-визитности [7] Если для каждого символа дано разбиение его атрибутов по визитам, то алгоритм вычисления атрибутов дерева принимает следующий вид:.
Алгоритм B.5. Вычисление атрибутов в простой многовизитной грамматике.
procedure визит_в_поддерево(n, i); begin вычислить наследуемые атрибуты I(Xn); визит_в_поддерево (nj1, ij1); ... визит_в_поддерево (njm, ijm); вычислить синтезируемые атрибуты S(Xn) end; beginforj := 1tok(Xr)do визит_в_поддерево (r, j){r - корень} end:
Среди всех формальных методов описания
Среди всех формальных методов описания языков программирования атрибутные грамматики получили, по- видимому, наибольшую известность и распространение. Причиной этого является то, что формализм атрибутных грамматик основывается на дереве разбора программы в КС-грамматике, что сближает его с хорошо разработанной теорией и практикой построения трансляторов. Вместе с тем выяснилось, что реализация вычислителей для атрибутных грамматик общего вида сталкивается с большими трудностями. В связи с этим было сделано множество попыток рассматривать те или иные классы атрибутных грамматик, обладающими "хорошими" свойствами. К числу таких свойств относятся, прежде всего, простота алгоритма проверки атрибутной грамматики на зацикленность и простота алгоритма вычисления атрибутов для атрибутных грамматик данного класса. В предлагаемой статье дается обзор работ, посвященных этим вопросам.
Вычислительные последовательности и корректность. Определение визита
Назовем вычислительной последовательностью [4] для дерева вывода t в AG последовательность вида:
cs = (n1, A1)(n2, A2)(n2, A2) ... (nr, Ar);
где
nj - внутренняя вершина t (в частности, корень);если nj#nj + 1, то nj + 1 - отец, сын или брат nj ;Aj - либо подмножество синтезируемых атрибутов nj , либо подмножество наследуемых атрибутов (то есть либо либо Aj



Bj




Таким образом при входе "вниз" в поддерево вычисляются некоторые наследуемые атрибуты корня поддерева, при возврате из поддерева вычисляются некоторые синтезируемые атрибуты корня поддерева.
Назовем незацикленную атрибутную грамматику корректной, если для всякого еe атрибутированного дерева существует вычислительная последовательность.
Теорема B.4. Незацикленная атрибутная грамматика корректна тогда и только тогда, когда для каждого правила p : X0




Теорема B.5. Сложность проверки незацикленной атрибутной грамматики на корректность линейна по размеру атрибутной грамматики.
Пусть t - дерево вывода и n - его внутренняя вершина. Рассмотрим вычислительную последовательность для t вида cs = cs1<n, B1>cs2<n, B2>cs3, где n входит в cs1 чeтное число раз, и не входит в cs2. Последовательность cs2 обходит поддерево с корнем n. Будем говорить, что <n, B1>cs2<n, B2> определяет визит в поддерево с корнем n и что вершина n в результате этого визита посещается один раз. Таким образом, если n входит в cs 2h раз, то n посещается h раз.
