Место компилятора в программном обеспечении
Место компилятора в программном обеспечении Компиляторы составляют существенную часть программного обеспечения ЭВМ. Это связано с тем, что языки высокого уровня стали основным средством разработки программ. Сегодня только очень малая часть программного обеспечения, требующая особой эффективности, разрабатывается с помощью ассемблеров. В настоящее время имеет применение довольно много языков программирования. Наряду с традиционными языками, такими, например, как Фортран, широкое распространение получили так называемые "универсальные" языки (Паскаль, Си, Модула-2, Ада и другие), а также некоторые специализированные (например, язык обработки списочных структур Лисп). Кроме того, большое распространение получили языки, связанные с узкими предметными областями, такие, как входные языки пакетов прикладных программ.
Для ряда названных языков имеется довольно много реализаций. Так, на рынке программного обеспечения представлены десятки реализаций языков Паскаля, Модулы-2 или Си для ЭВМ типа IBM PC.
С другой стороны, постоянно растущая потребность в новых компиляторах связана с бурным развитием архитектур ЭВМ. Это развитие идет по различным направлениям. Наряду с возникновением новых архитектур, совершенствуются старые архитектуры как в концептуальном отношении, так и по отдельным, конкретным параметрам. Это можно проиллюстрировать на примере микропроцессора Intel-80X86. Последовательные версии этого микропроцессора 8086, 80186, 80286, 80386, 80486, 80586 отличаются не только техническими характеристиками, но и, что более важно, новыми возможностями и, значит, изменением (расширением) системы команд. Естественно, это требует новых компиляторов (или модификации старых). То же можно сказать о микропроцессорах Motorola 68010, 68020, 68030, 68040.
В рамках традиционных последовательных машин развивается большое число различных направлений архитектур. Примерами могут служить архитектуры CISC, RISC. Такие ведущие фирмы, как Intel, Motorola, Sun, начинают переходить на выпуск машин с RISC- архитектурами. Естественно, для каждой новой системы команд требуется полный набор новых компиляторов с распространенных языков.
Наконец, бурно развиваются различные параллельные архитектуры. Среди них отметим векторные, многопроцессорные, с широким командным словом архитектуры (вариантом которых являются суперскалярные ЭВМ). На рынке уже имеются десятки типов ЭВМ с параллельной архитектурой, начиная от супер-ЭВМ (Cray, CDC и другие), через рабочие станции (например, IBM RS/6000) и кончая персональными компьютерами (например, на основе микропроцессора I-860). Естественно, для каждой из новых машин создаются новые компиляторы для многих языков программирования. Здесь необходимо также отметить, что новые архитектуры требуют разработки совершенно новых подходов к созданию компиляторов, так что наряду с собственно разработкой компиляторов ведется и большая научная работа по созданию новых методов
Структура компилятора
Обобщенная структура компилятора и основные фазы компиляции показаны на рис. 1.1
На начальной фазе лексического анализа входная программа, представляющая собой поток литер, разбивается на лексемы - слова в соответствии с определениями языка. Основными формализмами, лежащим в основе реализации лексических анализаторов, являются конечные автоматы и регулярные выражения. Лексический анализатор может работать в двух основных режимах: либо как подпрограмма, вызываемая синтаксическим анализатором для получения очередной лексемы, либо как полный проход, результатом которого является файл лексем.
В процессе выделения лексем лексический анализатор может как самостоятельно строить таблицы объектов (чисел, строк, идентификаторов и так далее), так и выдавать значения для каждой лексемы при очередном к нему обращении. В этом случае таблицы объектов строятся в последующих фазах (например, в процессе синтаксического анализа).
На этапе лексического анализа обнаруживаются некоторые (простейшие) ошибки (недопустимые символы, неправильная запись чисел, идентификаторов и другие).
Центральная задача синтаксического анализа - разбор структуры программы. Как правило, под структурой понимается дерево, соответствующее разбору в контекстно- свободной грамматике языка. В настоящее время чаще всего используется либо LL(1)-анализ (и его вариант - рекурсивный спуск), либо LR(1)-анализ и его варианты (LR(0), SLR(1), LALR(1) и другие). Рекурсивный спуск чаще используется при ручном программировании синтаксического анализатора, LR(1) - при использовании систем автоматического построения синтаксических анализаторов.
Результатом синтаксического анализа является синтаксическое дерево со ссылками на таблицы объектов. Ошибки, связанные со структурой программы, также обнаруживаются в процессе синтаксического анализа. На этапе контекстного анализа выявляются зависимости между частями программы, которые не могут быть описаны контекстно-свободным синтаксисом. Это, в основном, связи "описание-использование", в частности, анализ типов объектов, анализ областей видимости, соответствие параметров, метки и другие.
В процессе контекстного анализа таблицы объектов пополняются информацией об описаниях (свойствах) объектов.
Основным формализмом, используемым при контекстном анализе, является аппарат атрибутных грамматик. Результатом контекстного анализа является атрибутированное дерево программы. Информация об объектах может быть как рассредоточена в самом дереве, так и сосредоточена в отдельных таблицах объектов. В процессе контекстного анализа также могут быть обнаружены ошибки, связанные с неправильным использованием объектов.
Затем программа может быть переведена во внутреннее представление. Это делается для целей оптимизации и/или удобства генерации кода. Еще одной целью преобразования программы во внутреннее представление является желание иметь переносимый компилятор. Тогда только последняя фаза (генерация кода) является машинно-зависимой. В качестве внутреннего представления может использоваться префиксная или постфиксная запись, ориентированный граф, тройки, четверки и другие способы.
Фаз оптимизации может быть несколько. Оптимизации обычно делят на машинно-зависимые и машинно-независи- мые, локальные и глобальные. Определенная часть машин- но-зависимой оптимизации выполняется на фазе генерации кода. Глобальная оптимизация пытается принять во внимание структуру всей программы, локальная - только небольших ее фрагментов. Глобальная оптимизация основывается на глобальном потоковом анализе, который выполняется на графе программы и представляет по существу преобразование этого графа. При этом могут учитываться такие свойства программы, как межпроцедурный анализ, межмодульный анализ, анализ областей жизни переменных и так далее.
Наконец, генерация кода - последняя фаза трансляции. Результатом ее является либо ассемблерный модуль, либо объектный (или загрузочный) модуль. В процессе генерации кода могут выполняться некоторые локальные оптимизации, такие как распределение регистров, выбор длинных или коротких переходов, учет стоимости команд при выборе конкретной последовательности команд.Для генерации кода разработаны различные методы, такие как таблицы решений, сопоставление образцов, включающее динамическое программирование, различные синтаксические методы. Конечно, те или иные фазы транслятора могут либо отсутствовать совсем, либо объединяться. В простейшем случае однопроходного транслятора нет явной фазы генерации промежуточного представления и оптимизации, остальные фазы объединены в одну, причем нет и явно построенного синтаксического дерева.

увеличить изображение
Рис. 1.1.
Алфавиты, цепочки и языки
Алфавит, или словарь - это конечное множество символов. Для обозначения символов мы будем пользоваться цифрами, латинскими буквами и специальными литерами типа

Пусть V - алфавит. Цепочка в алфавите V - это любая строка конечной длины, составленная из символов алфавита V . Синонимом цепочки являются предложение, строка и слово. Пустая цепочка (обозначается e) - это цепочка, в которую не входит ни один символ.
Конкатенацией цепочек x и y называется цепочка xy. Заметим, что xe = ex = x для любой цепочки x.
Пусть x, y, z - произвольные цепочки в некотором алфавите. Цепочка y называется подцепочкой цепочки xyz. Цепочки x и y называются, соответственно, префиксом и суффиксом цепочки xy. Заметим, что любой префикс или суффикс цепочки является подцепочкой этой цепочки. Кроме того, пустая цепочка является префиксом, суффиксом и подцепочкой для любой цепочки.
Пример 2.1. Для цепочки abbba префиксом является любая цепочка из множества

суффиксом является любая цепочка из множества

подцепочкой является любая цепочка из множества

Длиной цепочки w (обозначается |w|) называется число символов в ней. Например, |abababa| = 7, а |e| = 0. Язык в алфавите V - это некоторое множество цепочек в алфавите V .
Пример 2.2. Пусть дан алфавит V = {a, b}. Вот некоторые языки в алфавите V:







Два последних языка содержат бесконечное число цепочек.
Введем обозначение




Пример 2.3. Пусть


Введем некоторые операции над языками.
Пусть


Конкатенацией языков



Пусть L - язык в алфавите V . Итерацией языка L называется язык

 | (1) |
 | (2) |
 | (3) |
Пример 2.4. Пусть




Большинство языков, представляющих интерес, содержат бесконечное число цепочек. При этом возникают три важных вопроса.
Во-первых, как представить язык (то есть специфицировать входящие в него цепочки)? Если язык содержит только конечное множество цепочек, ответ прост. Можно просто перечислить его цепочки. Если язык бесконечен, необходимо найти для него конечное представление. Это конечное представление, в свою очередь, будет строкой символов над некоторым алфавитом вместе с некоторой интерпретацией, связывающей это представление с языком.
Во-вторых, для любого ли языка существует конечное представление? Можно предположить, что ответ отрицателен. Мы увидим, что множество всех цепочек над алфавитом счетно. Язык - это любое подмножество цепочек. Из теории множеств известно, что множество всех подмножеств счетного множества несчетно. Хотя мы и не дали строгого определения того, что является конечным представлением, интуитивно ясно, что любое разумное определение конечного представления ведет только к счетному множеству конечных представлений, поскольку нужно иметь возможность записать такое конечное представление в виде строки символов конечной длины. Поэтому языков значительно больше, чем конечных представлений.
В-третьих, можно спросить, какова структура тех классов языков, для которых существует конечное представление?
Формальное определение грамматики
Для нас наибольший интерес представляет одна из систем генерации языков - грамматики. Понятие грамматики изначально было формализовано лингвистами при изучении естественных языков. Предполагалось, что это может помочь при их автоматической трансляции. Однако, наилучшие результаты в этом направлении достигнуты при описании не естественных языков, а языков программирования. Примером может служить способ описания синтаксиса языков программирования при помощи БНФ - формы Бэкуса-Наура.
Определение. Грамматика - это четверка G = (N,T,P,S), где
(1) N - алфавит нетерминальных символов;
(2) T - алфавит терминальных символов,

(3) P - конечное множество правил вида


(4)

Мы будем использовать большие латинские буквы для обозначения нетерминальных символов, малые латинские буквы из начала алфавита для обозначения терминальных символов, малые латинские буквы из конца алфавита для обозначения цепочек из


Будем использовать также сокращенную запись


Определим на множестве








Мы будем использовать также рефлексивно-транзитивное и транзитивное замыкания отношения







выводима (нетривиально выводима, выводима за k шагов) из

Если


где






Сентенциальной формой грамматики G называется цепочка, выводимая из ее начального символа.
Языком, порождаемым грамматикой G (обозначается L(G)), называется множество всех ее терминальных сентенциальных форм, то есть

Грамматики G1 и G2 называются эквивалентными, если они порождают один и тот же язык, то есть

Пример 2.5. Грамматика G = ({S, B, C}, {a, b, c}, P, S), где


Действительно, применяем n - 1 раз правило 1 и получаем



Затем используем правило 4 и получаем anbBn-1Cn . Затем применяем n - 1 раз правило 5 и получаем anbnCn. Затем применяем правило 6 и n - 1 раз правило 7 и получаем anbncn . Можно показать, что язык L(G) состоит из цепочек только такого вида.
Пример 2.6. Рассмотрим грамматику



Нетрудно показать, что грамматика порождает язык

Пример 2.7. Рассмотрим грамматику


Класс рекурсивных множеств
Теперь можно показать, что класс рекурсивных множеств является собственным подклассом класса рекурсивно перечислимых множеств. То есть существует множество, слова которого могут быть распознаны машиной Тьюринга, которая не останавливается на некоторых словах, не принадлежащих множеству, но не может быть распознано никакой машиной Тьюринга, которая останавливается на всех словах. Примером такого множества является дополнение к L1.
Лемма 2.1. Если множество рекурсивно, то и его дополнение рекурсивно.
Доказательство. Если L - рекурсивное множество,

симулирует Tm. Кроме того, для каждой пары, составленной из недопускающего состояния и ленточного символа Tm, для которых у Tm переход не определен, Tm1 переходит в состояние q и затем останавливается.
Таким образом Tm1 симулирует Tm вплоть до остановки. Если Tm останавливается в одном из допускающих состояний, Tm1 останавливается без допуска. Если Tm останавливается в одном из недопускающих состояний, значит не допускает вход. Тогда Tm1 делает еще один переход в состояние q и допускает. Ясно, что Tm1 допускает T*\L.
Лемма 2.2. Пусть



Доказательство. Слова L2 допускаются некоторой Tm, работающей следующим образом. Отметим, что Tm не обязательно останавливается на словах не из L2.
Если дано x,Tm перечисляет предложения x1, x2,... пока не найдет xi = x, определяя тем самым, что x - это i-е слово в перечислении.Tm генерирует Tmi и передает управление универсальной машине Тьюринга, которая симулирует Tmi со входом x.Если Tmi останавливается со входом xi и допускает, Tm останавливается и допускает; если Tmi останавливается и отвергает xi, то Tm останавливается и отвергает xi.
Наконец, если Tmi не останавливается, то Tm не останавливается.Таким образом L2 рекурсивно перечислимо, поскольку L2 - это множество допускаемое Tm. Но дополнение к


тогда и только тогда, когда xj не допускается Tmj . Это противоречит утверждению, что

Теорема 2.3. Существует рекурсивно перечислимое множество, не являющееся рекурсивным.
Доказательство. Доказательство. По лемме 2.2 L2 - рекурсивно перечислимое множество, дополнение которого не рекурсивно перечислимо. Если бы L2 было рекурсивно, по лемме

Линейно-ограниченные автоматы и их связь с контекстно-зависимыми грамматиками
Каждый КЗ-язык является рекурсивным, но обратное не верно. Покажем что существует алгоритм, позволяющий для произвольного КЗ-языка L в алфавите T, и произвольной цепочки

Теорема 2.6. Каждый контекстно-зависимый язык является рекурсивным языком.
Доказательство. Пусть L - контекстно-зависимый язык. Тогда существует некоторая неукорачивающая грамматика G = (N, T, P, S), порождающая L.
Пусть


Определим множество Tm как множество строк


Легко показать, что Tm можно получить из Tm-1
просматривая, какие строки с длиной, меньшей или равной n можно вывести из строк из Tm-1 применением одного правила, то есть

Если


Очевидно, что



Покажем, что существует такое m, что Tm = Tm-1. Поскольку для каждого i > 1 справедливо







Линейно-ограниченный автомат (ЛОА) - это недетерминированная машина Тьюринга с одной лентой, которая никогда не выходит за пределы |w| ячеек, где w - вход. Формально, линейно-ограниченный автомат обозначается как

Q - это множество состояний,




? содержит два специальных символа, обычно обозначаемых © и $, - левый и правый концевые маркеры, соответственно. Эти символы располагаются сначала по концам входа и их функция - предотвратить переход головки за пределы области, в которой расположен вход.
Конфигурация M и отношение

(q,A1A2,...,An,i) где


Будем говорить, что



То есть M печатает A поверх Ai, меняет состояние на p и передвигает головку влево или вправо, но не за пределы области, в которой символы располагались исходно. Как обычно, определим отношение


Если


то

Язык, допускаемый M - это



Будем называть M детерминированным, если D(q, A) содержит не более одного элемента для любых

Класс множеств, допускаемых ЛОА, в точности совпадает с классом контекстно - зависимых языков.
Теорема 2.7. Если L - контекстно-зависимый язык, то L допускается ЛОА.
Доказательство. Пусть G = (VN, VT, P, S) - контекстно- зависимая грамматика. Построим ЛОА M такой, что он допускает язык L(G). Не вдаваясь в детали построения M, поскольку он довольно сложен, рассмотрим схему его работы. В качестве ленточных символов будем рассматривать пары

Цепочку символов

n будем называть " первым треком ",

n - " вторым треком ". Первый трек будет содержать входную строку x с концевыми маркерами. Второй трек будет использоваться для вычислений. На первом шаге M помещает символ S в самой левой ячейке второго трека. Затем M выполняет процедуру генерации в соответствии со следующими шагами:
Процедура выбирает подстроку символов




На выходе из процедуры первый трек все еще содержит строку x, а второй трек содержит строку ? такую, что

Если

Отметим схожесть этих рассуждений и рассуждений в случае произвольной грамматики. Тогда промежуточные сентенциальные формы могли иметь длину, произвольно большую по сравнению с длиной входа. Как следствие, требовалась вся мощь машин Тьюринга. В случае контекстно- зависимых грамматик промежуточные сентенциальные формы не могут быть длиннее входа.
Теорема 2.8. Если L допускается ЛОА, то L - контекстно - зависимый язык.
Доказательство. Конструкция КЗГ по ЛОА аналогична конструкции грамматики типа 0, моделирующей машину Тьюринга. Различие заключатся в том, что нетерминалы КЗГ должны указывать не только текущее и исходное содержимое ячеек ленты ЛОА, но и то, является ли ячейка соседней справа или слева с концевым маркером.
Кроме того, состояние ЛОА должно комбинироваться с символом под головкой, поскольку КЗГ не может иметь раздельные символы для концевых маркеров и состояния ЛОА, так как эти символы должны были бы быть заменены на e, когда строка превращается в терминальную.
Теорема 2.9. Существуют рекурсивные множества, не являющиеся контекстно - зависимыми.
Доказательство. Все строки в {0,1}* можно занумеровать. Пусть xi - i-ое слово. Мы можем занумеровать все грамматики типа 0, терминальными символами которых являются 0 и 1. Поскольку имена переменных не важны и каждая грамматика имеет конечное их число, можно предположить, что существует счетное число переменных.
Представим переменные в двоичной кодировке как 01, 011, 0111, 01111 и т.д. Предположим, что 01 всегда является стартовым символом. Кроме того, в этой кодировке терминал 0 будет представляться как 00, а терминал 1 как 001. Символ «

Отметим, что не все строки из 0 и 1 представляют грамматики, и не обязательно КЗГ. Однако, по данной строке легко можно сказать, представляет ли она КЗГ. i- ю грамматику можно найти, генерируя двоичные строки в описанном порядке пока не сгенерируется i-я строка, являющаяся КЗГ. Поскольку имеется бесконечное число КЗГ, их можно занумеровать в некотором порядке G1, G2, ...
Определим L = {xi|xi

Покажем теперь, что L не генерируется никакой КЗ-грамматикой.
Предположим, что L генерируется КЗ- грамматикой Gi. Во-первых, предположим, что






Машины Тьюринга
Формально машина Тьюринга (Tm) - это

Q - конечное множество состояний;



D функция переходов, отображение из



Рис. 2.2. Машина Тьюринга
Так определенная машина Тьюринга называется детерминированной. Недетерминированная машина Тьюринга для каждой пары




Шаг Tm определим следующим образом.
Пусть (q, A1, A2, ... An, i) - конфигурация Tm,
где

Если

(R от англ. Right), то


То есть Tm печатает символ A и передвигается вправо.
Если


(L от англ. Left), то если i = n, то допустимо A = B и

Tm печатает A и передвигается влево, но не за конец ленты.
Если i = n + 1, головка просматривает пустой символ B.
Если D(q, B) = (p, A, R), то


Если D(q, B) = (p, A, L), то допустимо A=B и

Если две конфигурации связаны отношением


Язык, допускаемый Tm, это множество таких слов из T*, которые будучи расположены в левом конце ленты переводят Tm из начального состояния q0 с начальным положением головки в самом левом конце ленты в конечное состояние. Формально, язык, допускаемй Tm, это

Если Tm распознает L, то Tm останавливается, то есть не имеет переходов после того, как слово допущено. Однако, если слово не допущено, возможно, что Tm не останавливается.
Язык, допускаемый некоторой Tm, называется рекурсивно перечислимым. Если Tm останавливается на всех входах, то говорят, что Tm задает алгоритм и язык называется рекурсивным.
Существует машина Тьюринга, которая по некоторому описанию произвольной Tm и кодированию слова x моделирует поведение Tm со входом x. Такая машина Тьюринга называется универсальной машиной Тьюринга.
Неразрешимость проблемы останова
Проблема останова для машины Тьюринга формулируется следующим образом: можно ли определить по данной машине Тьюринга в произвольной конфигурации со строкой конечной длины непустых символов на ленте остановится ли она? Говорят, что эта проблема рекурсивно неразрешима, что означает, что не существует алгоритма, который для любой Tm в произвольной конфигурации определял бы остановится ли в конце концов Tm.
Перенумеруем все машины Тьюринга и все возможные входы над алфавитом

L1={xi|xi не допускается Ti}
Ясно, что






допускает



Представление языков
Процедура - это конечная последовательность инструкций, которые могут быть механически выполнены. Примером может служить машинная программа. Процедура, которая всегда заканчивается, называется алгоритмом.
Один из способов представления языка - дать алгоритм, определяющий, принадлежит ли цепочка языку. Более общий способ состоит в том, чтобы дать процедуру, которая останавливается с ответом "да" для цепочек, принадлежащих языку, и либо останавливается с ответом "нет", либо вообще не останавливается для цепочек, не принадлежащих языку. Говорят, что такая процедура или алгоритм распознает язык.
Такой метод представляет язык с точки зрения распознавания. Язык можно также представить методом порождения. А именно, можно дать процедуру, которая систематически порождает в определ_нном порядке цепочки языка.
Если мы можем распознать цепочки языка над алфавитом V либо с помощью процедуры, либо с помощью алгоритма, то мы можем и генерировать язык, поскольку мы можем систематически генерировать все цепочки из

Предположим, что V имеет p символов. Мы можем рассматривать цепочки из


Пусть P - процедура для проверки принадлежности цепочки языку L. Предположим, что P может быть представлена дискретными шагами, так что имеет смысл говорить об i-ом шаге процедуры для любой данной цепочки. Прежде чем дать процедуру перечисления цепочек языка L, дадим процедуру нумерации пар положительных чисел.
Все упорядоченные пары положительных чисел (x, y) можно отобразить на множество положительных чисел следующей формулой:
z = (x + y - 1)(x + y - 2)/2 + y
Пары целых положительных чисел можно упорядочить в соответствии со значением z (рис. 2.1, б).
что язык распознается машиной Тьюринга
Докажем, что язык распознается машиной Тьюринга тогда и только тогда, когда он генерируется грамматикой типа 0. Для доказательства части "если" мы построим недетерминированную машину Тьюринга, которая будет Связь машин Тьюринга и грамматик типа 0 35 недетерминированно выбирать выводы в грамматике и смотреть, является ли вывод входом. Если да, машина допускает вход.
Для доказательства части "только если" мы построим грамматику, которая недетерминированно генерирует представления терминальной строки и затем симулирует машину Тьюринга на этой строке. Если строка допускается некоторой Tm, строка конвертируется в терминальные символы, которые она представляет.
Теорема 2.4. Если L генерируется грамматикой типа 0, то L распознается машиной Тьюринга.
Доказательство. Пусть


где

Предполагается, что последние три символа не входят в

Вначале Tm содержит на входной ленте

Теперь Tm недетерминированно симулирует вывод в G, начиная с S. Каждая сентенциальная форма вывода появляется по порядку между последними двумя #. Если некоторый выбор переходов ведет к терминальной строке, она сравнивается с w. Если они совпадают, Tm допускает.
Формально, пусть Tm имеет на ленте #w#A1A2...Ak#. Tm передвигает недетерминированно головку по A1A2...Ak, выбирая позицию i и константу r между 1 и максимальной длиной левой части любого правила вывода в P. Затем Tm проверяет подстроки AiAi+1...Ai+r-1. Если AiAi+1...Ai+r-1
- левая часть некоторого правила вывода из P, она может быть заменена на правую часть. Tm может сдвинуть Ai+rAi+r+1...Ak# либо влево, либо вправо, освобождая или заполняя место, если правая часть имеет длину, отличную от r.
Из этой простой симуляции выводов в G видно, что Tm печатает на ленте строку вида


Теорема 2.5. Если L распознается некоторой машиной Тьюринга,то L генерируется грамматикой типа 0.
Доказательство. Пусть


и затем симулирует поведение Tm на одной из копий. Если Tm допускает слово, то G трансформирует вторую копию в терминальную строку. Если Tm не допускает L, то вывод никогда не приводит к терминальной строке.
Формально, пусть


Продукции таковы:















Используя правила 1 и 2

где


Предположим, что Tm допускает строку a1a2 ... an. Тогда для некоторого m Tm использует не более, чем m ячеек справа от входа. Используя правило 3, затем правило 4 m раз, и наконец, правило 5, имеем

Начиная с этого момента могут быть использованы только правила 6 и 7, пока не сгенерируется допускающее состояние. Отметим, что первые компоненты ленточных символов в




где a1, a2, ... an принадлежат

X1 X2, ...Xn+m принадлежат

Предположение индукции тривиально для нуля шагов. Предположим, что оно справедливо для k - 1 шагов. Пусть

за k шагов. По предположению индукции

Пусть E = L, если j2 = j1 - 1 и E = R, если j2 = j1 + 1. В этом случае D(q1, Xj1 ) = (q2, Yj1, E).
По правилам 6 или 7


в зависимости от того, равно ли E значению R или L.
Теперь Xi = Yi для всех

Таким образом,

что доказывает предположение индукции.
По правилу 8, если


Таким образом, G может генерировать a1a2 ... an, если a1a2 ... an допускается Tm. Таким образом, L(G) включает все слова, допускаемые Tm. Для завершения доказательства необходимо показать, что все слова из L(G) допускаются Tm. Индукцией доказывается, что

Типы грамматик и их свойства
Рассмотрим классификацию грамматик (предложенную Н.Хомским), основанную на виде их правил.
Определение. Пусть дана грамматика G = (N, T, P, S). Тогда
(1) если правила грамматики не удовлетворяют никаким ограничениям, то ее называют грамматикой типа 0, или грамматикой без ограничений.
(2) если
каждое правило грамматики, кроме




(3) если каждое правило грамматики имеет вид


(4) если каждое правило грамматики имеет вид либо



Легко видеть, что грамматика в примере 2.5 - неукорачивающая, в примере 2.6 - контекстно-свободная, в примере 2.7 - праволинейная.
Язык, порождаемый грамматикой типа i, называют языком типа i. Язык типа 0 называют также языком без ограничений, язык типа 1 - контекстно-зависимым (КЗ), язык типа 2 - контекстно-свободным (КС), язык типа 3 - праволинейным.
Конечные автоматы
Регулярные выражения, введенные ранее, служат для описания регулярных множеств. Для распознавания регулярных множеств служат конечные автоматы. Недетерминированный конечный автомат (НКА) - по определению есть пятерка M = (Q, T, D, q0, F), где
Q - конечное множество состояний,T - конечное множество допустимых входных символов (входной алфавит),D - функция переходов (отображающая множество



Работа конечного автомата представляет собой некоторую последовательность шагов, или тактов. Такт определяется текущим состоянием управляющего устройства и входным символом, обозреваемым в данный момент входной головкой. Сам шаг состоит из изменения состояния и, возможно, сдвига входной головки на одну ячейку вправо (рис. 3.2.).
Недетерминизм автомата заключается в том, что, во- первых, находясь в некотором состоянии и обозревая текущий символ, автомат может перейти в одно из, вообще говоря, нескольких возможных состояний, и во-вторых, автомат может делать переходы по e.

Рис. 3.2.
Пусть M = (Q, T, D, q0, F) - НКА. Конфигурацией автомата M называется пара






Будем обозначать символом





Важным частным случаем недетерминированного конечного автомата является детерминированный конечный автомат, который на каждом такте работы имеет возможность перейти не более чем в одно состояние и не может делать переходы по e.
Пусть M = (Q, T, D, q0, F) - НКА. Будем называть M детерминированным конечным автоматом (ДКА), если выполнены следующие два условия:
D(q, e) =




Так как функция переходов ДКА содержит не более одного элемента для любой пары аргументов, для ДКА мы будем пользоваться записью D(q, a)=p вместо D(q, a)={p}.
Конечный автомат может быть изображен графически в виде диаграммы, представляющей собой ориентированный граф, в котором каждому состоянию соответствует вершина, а дуга, помеченная символом


Пример 3.3. Пусть L = L(r), где r = (a|b)*a(a|b)(a|b).
Недетерминированный конечный автомат M, допускающий язык L:
M = {{1, 2, 3, 4}, {a, b}, D, 1, {4}},
где функция переходов D определяется так:

Диаграмма автомата приведена на рис. 3.3 а.Детерминированный конечный автомат M, допускающий язык L:
M = {{1, 2, 3, 4, 5, 6, 7, 8}, {a, b}, D, 1, {3, 5, 6, 8}}
где функция переходов D определяется так:

Диаграмма автомата приведена на рис. 3.3 б.

Рис. 3.3.
Пример 3.4. Диаграмма автомата, допускающего множество чисел в десятичной записи, приведена на рис. 3.4.

Рис. 3.4.
Пример 3.5. Анализ цепочек.
При анализе цепочки w = ababa автомат из примера рис. 3.3, а, может сделать следующую последовательность тактов:

Состояние 4 является заключительным, отсюда, цепочка w допускается этим автоматом.При анализе цепочки w = ababab автомат из примера рис. 3.3, б, должен сделать следующую последовательность тактов:

Так как состояние 7 не является заключительным, цепочка w не допускается этим автоматом.
Конструктор лексических анализаторов LEX
Для автоматизации разработки ЛА было создано довольно много средств. Как правило, входным языком для них служат или праволинейные грамматики, или язык регулярных выражений. Одной из наиболее распространенных систем является LEX, работающий с расширенными регулярными выражениями. LEX-программа состоит из трех частей:
Объявления %% Правила трансляции %%
Вспомогательные подпрограммы Секция объявлений включает объявления переменных, констант и определения регулярных выражений. При определении регулярных выражений могут использоваться следующие конструкции:
| [abc] | - либо a, либо b, либо c, |
| [a-z] | - диапазон символов, |
| R* | - 0 или более повторений регулярного выражения R, |
| R+ | - 1 или более повторений регулярного выражения R, |
| R1/R2 | - R1, если за ним следует R2, |
| R1|R2 | - либо R1, либо R2, |
| R? | - если есть R, выбрать его, |
| R$ | - выбрать R, если оно последнее в строке, |
| ^R | - выбрать R, если оно первое в строке, |
| [^R] | - дополнение к R, |
| R{n,m} | - повторение R от n до m раз, |
| {имя} | - именованное регулярное выражение, |
| (R) | - группировка. |
Правила трансляции LEX-программ имеют вид
p_1 { действие_1 } p_2 { действие_2 } ................ p_n { действие_n }
где p_i - регулярное выражение, а действие_i - фрагмент программы, описывающий, какое действие должен сделать ЛА, когда образец p_i сопоставляется лексеме. В LEX действия записываются на Си.
Третья секция содержит вспомогательные процедуры, необходимые для действий. Эти процедуры могут транслироваться раздельно и загружаться с ЛА.
ЛА, сгенерированный LEX, взаимодействует с синтаксическим анализатором следующим образом. При вызове его синтаксическим анализатором ЛА посимвольно читает остаток входа, пока не находит самый длинный префикс, который может быть сопоставлен одному из регулярных выражений p_i. Затем он выполняет действие_i. Как правило, действие_i возвращает управление синтаксическому анализатору. Если это не так, то есть в соответствующем действии нет возврата, то ЛА продолжает поиск лексем до тех пор, пока действие не вернет управление синтаксическому анализатору.
Повторный поиск лексем вплоть до явной передачи управления позволяет ЛА правильно обрабатывать пробелы и комментарии.
Синтаксическому анализатору ЛА возвращает единственное значение - тип лексемы. Для передачи информации о типе лексемы используется глобальная переменная yylval. Текстовое представление выделенной лексемы хранится в переменной yytext, а ее длина в переменной yylen.
Пример 3.11. LEX-программа для ЛА, обрабатывающего идентификаторы, числа, ключевые слова if, then, else и знаки логических операций.
%{ /*определения констант LT,LE,EQ,NE,GT, GE,IF,THEN,ELSE,ID,NUMBER,RELOP, например, через DEFINE или скалярный тип*/ %} /*регулярные определения*/ delim [ \t\n] ws {delim}+ letter [A-Za-z] digit [0-9] id {letter}({letter}|{digit})* number {digit}+(\.{digit}+)?,(E[+\-]?;,{digit}+)?;, %% {ws} {/* действий и возврата нет */} if {return(IF),} then {return(THEN),} else {return(ELSE),} {id} {yylval=install_id(), return(ID),} {number} {yylval=install_num(), return(NUMBER),} "<" {yylval=LT, return(RELOP),} "<=" {yylval=LE, return(RELOP),} "=" {yylval=EQ, return(RELOP),} "<>" {yylval=NE, return(RELOP),} ">" {yylval=GT, return(RELOP),} ">=" {yylval=GE, return(RELOP),} %% install_id() {/*подпрограмма, которая помещает лексему, на первый символ которой указывает yytext, длина которой равна yylen, в таблицу символов и возвращает указатель на нее*/ } install_num() {/*аналогичная подпрограмма для размещения лексемы числа*/ }
В разделе объявлений, заключенном в скобки %{ и %}, перечислены константы, используемые правилами трансляции. Все, что заключено в эти скобки, непосредственно копируется в программу ЛА lex.yy.c и не рассматривается как часть регулярных определений или правил трансляции. То же касается и вспомогательных подпрограмм третьей секции. В данном примере это подпрограммы install_id и install_num.
В секцию определений входят также некоторые регулярные определения. Каждое такое определение состоит из имени и регулярного выражения, обозначаемого этим именем.
Например, первое определенное имя - это delim. Оно обозначает класс символов { \t\n\}, то есть любой из трех символов: пробел, табуляция или новая строка. Второе определение - разделитель, обозначаемый именем ws. Разделитель - это любая последовательность одного или более символов-разделителей. Слово delim должно быть заключено в скобки, чтобы отличить его от образца, состоящего из пяти символов delim.
В определении letter используется класс символов. Сокращение [A-Za-z] означает любую из прописных букв от A до Z или строчных букв от a до z. В пятом определении для id для группировки используются скобки, являющиеся метасимволами LEX. Аналогично, вертикальная черта - метасимвол LEX, обозначающий объединение.
В последнем регулярном определении number символ "+" используется как метасимвол "одно или более вхождений", символ "?" как метасимвол "ноль или одно вхождение". Обратная черта используется для того, чтобы придать обычный смысл символу, использующемуся в LEX как метасимвол. В частности, десятичная точка в определении number обозначается как "\", поскольку точка сама по себе представляет класс, состоящий из всех символов, за исключением символа новой строки. В классe символов [+\] обратная черта перед минусом стоит потому, что знак минус используется как символ диапазона, как в [A-Z].
Если символ имеет смысл метасимвола, то придать ему обычный смысл можно и по-другому, заключив его в кавычки. Так, в секции правил трансляции шесть операций отношения заключены в кавычки.
Рассмотрим правила трансляции, следующие за первым %%. Согласно первому правилу, если обнаружено ws, то есть максимальная последовательность пробелов, табуляций и новых строк, никаких действий не производится. В частности, не осуществляется возврат в синтаксический анализатор.
Согласно второму правилу, если обнаружена последовательность букв "if", нужно вернуть значение IF, которое определено как целая константа, понимаемая синтаксическим анализатором как лексема "if".
Аналогично обрабатываются ключевые слова "then" и "else" в двух следущих правилах.
В действии, связанном с правилом для id, два оператора. Переменной yylval присваивается значение, возвращаемое процедурой install_id. Переменная yyl- val определена в программе lex.yy.c, выходе LEX, и она доступна синтаксическому анализатору. yylval хранит возвращаемое лексическое значение, поскольку второй оператор в действии, return(ID), может только возвратить код класса лексем. Функция install_id заносит идентификаторы в таблицу символов.
Аналогично обрабатываются числа в следующем правиле. В последних шести правилах yylval используется для возврата кода операции отношения, возвращаемое же функцией значение - это код лексемы relop.
Если, например, в текущий момент ЛА обрабатывает лексему "if", то этой лексеме соответствуют два образца: "if" и {id} и более длинной строки, соответствующей образцу, нет. Поскольку образец "if" предшествует образцу для идентификатора, конфликт разрешается в пользу ключевого слова. Такая стратегия разрешения конфликтов позволяет легко резервировать ключевые слова.
Если на входе встречается "<=", то первому символу соответствует образец <, но это не самый длинный образец, который соответствует префиксу входа. Стратегия выбора самого длинного префикса легко разрешает такого рода конфликты.
Лексический анализ
Основная задача лексического анализа - разбить входной текст, состоящий из последовательности одиночных символов, на последовательность слов, или лексем, то есть выделить эти слова из непрерывной последовательности символов. Все символы входной последовательности с этой точки зрения разделяются на символы, принадлежащие каким-либо лексемам, и символы, разделяющие лексемы (разделители). В некоторых случаях между лексемами может и не быть разделителей. С другой стороны, в некоторых языках лексемы могут содержать незначащие символы (например, символ пробела в Фортране). В Си разделительное значение символов-разделителей может блокироваться ("\" в конце строки внутри "...").
Обычно все лексемы делятся на классы. Примерами таких классов являются числа (целые, восьмеричные, шестнадцатиричные, действительные и т.д.), идентификаторы, строки. Отдельно выделяются ключевые слова и символы пунктуации (иногда их называют символы-ограничители). Как правило, ключевые слова - это некоторое конечное подмножество идентификаторов. В некоторых языках (например, ПЛ/1) смысл лексемы может зависеть от ее контекста и невозможно провести лексический анализ в отрыве от синтаксического.
Для осуществления двух дальнейших фаз анализа лексический анализатор выдает информацию двух типов: для синтаксического анализатора, работающего вслед за лексическим, существенна информация о последовательности классов лексем, ограничителей и ключевых слов, а для контекстного анализатора, работающего вслед за синтаксическим, существенна информация о конкретных значениях отдельных лексем (идентификаторов, чисел и т.д.).
Таким образом, общая схема работы лексического анализатора такова. Сначала выделяется отдельная лексема (при этом, возможно, используются символы- разделители). Ключевые слова распознаются явным выделением непосредственно из текста, либо сначала выделяется идентификатор, а затем делается проверка на принадлежность его множеству ключевых слов.
Если выделенная лексема является ограничителем, то этот ограничитель (точнее, некоторый его признак) выдается как результат лексического анализа.
Если выделенная лексема является ключевым словом, то выдается признак соответствующего ключевого слова. Если выделенная лексема является идентификатором - выдается признак идентификатора, а сам идентификатор сохраняется отдельно. Наконец, если выделенная лексема принадлежит какому-либо из других классов лексем (например, лексема представляет собой число, строку и т.д.), то выдается признак соответствующего класса, а значение лексемы сохраняется отдельно.
Лексический анализатор может быть как самостоятельной фазой трансляции, так и подпрограммой, работающей по принципу "дай лексему". В первом случае (рис. 3.1, а) выходом анализатора является файл лексем, во втором - (рис. 3.1., б) лексема выдается при каждом обращении к анализатору (при этом, как правило, признак класса лексемы возвращается как результат функции "лексический анализатор", а значение лексемы передается через глобальную переменную). С точки зрения обработки значений лексем, анализатор может либо просто выдавать значение каждой лексемы, при этом построение таблиц объектов (идентификаторов, строк, чисел и т.д.) переносится на более поздние фазы, либо он может самостоятельно строить таблицы объектов. В этом случае в качестве значения лексемы выдается указатель на вход в соответствующую таблицу.

Рис. 3.1.
Работа лексического анализатора задается некоторым конечным автоматом. Однако, непосредственное описание конечного автомата неудобно с практической точки зрения. Поэтому для задания лексического анализатора, как правило, используется либо регулярное выражение, либо праволинейная грамматика. Все три формализма (конечных автоматов, регулярных выражений и праволинейных грамматик) имеют одинаковую выразительную мощность. В частности, по регулярному выражению или праволинейной грамматике можно сконструировать конечный автомат, распознающий тот же язык.
Построение детерминированного конечного автомата по недетерминированному
Рассмотрим алгоритм построения по недетерминированному конечному автомату детерминированного конечного автомата, допускающего тот же язык.
Алгоритм 3.2. Построение детерминированного конечного автомата по недетерминированному.
Вход. НКА M = (Q, T, D, q0, F).
Выход. ДКА

Метод. Каждое состояние результирующего ДКА - это некоторое множество состояний исходного НКА.
В алгоритме будут использоваться следующие функции:




Вначале Q' и D' пусты. Выполнить шаги 1-4:
(1) Определить

(2) Добавить

(3) Выполнить следующую процедуру:

(4) Определить

Пример 3.6. Результат применения алгоритма 3.2 приведен на рис. 3.10.

Рис. 3.10.
Приведем теперь алгоритм построения по регулярному выражению детерминированного конечного автомата, допускающего тот же язык [?].
Пусть дано регулярное выражение r в алфавите T. К регулярному выражению r добавим маркер конца: (r)#. Такое регулярное выражение будем называть пополненным. В процессе своей работы алгоритм будет использовать пополненное регулярное выражение.
Алгоритм будет оперировать с синтаксическим деревом для пополненного регулярного выражения (r)# , каждый лист которого помечен символом

Каждому листу дерева (кроме e-листьев) присвоим уникальный номер, называемый позицией, и будем использовать его, с одной стороны, для ссылки на лист в дереве, и, с другой стороны, для ссылки на символ, соответствующий этому листу. Заметим, что если некоторый символ используется в регулярном выражении несколько раз, он имеет несколько позиций.
Обойдем дерево T снизу-вверх слева-направо и вычислим четыре функции: nullable,firstpos, lastpos и followpos. Три первые функции - nullable, firstpos и lastpos - определены на узлах дерева, а followpos - на множестве позиций. Значением всех функций, кроме nullable, является множество позиций. Функция followpos вычисляется через три остальные функции.
Функция firstpos(n) для каждого узла n синтаксического дерева регулярного выражения дает множество позиций, которые соответствуют первым символам в подцепочках, генерируемых подвыражением с вершиной в n. Аналогично, lastpos(n) дает множество позиций, которым соответствуют последние символы в подцепочках, генерируемых подвыражениями с вершиной n. Для узла n, поддеревья которого (то есть деревья, у которых узел n является корнем) могут породить пустое слово, определим nullable(n)=true, а для остальных узлов nullable(n)=false.
Таблица для вычисления функций nullable, firstpos и lastpos приведена на рис. 3.11.
Пример 3.7. На рис. 3.12 приведено cинтаксическое дерево для пополненного регулярного выражения (a|b)*abb# с результатом вычисления функций firstpos и lastpos. Слева от каждого узла расположено значение firstpos, справа от узла - значение lastpos. Заметим, что эти функции могут быть вычислены за один обход дерева.
Если i - позиция, то followpos(i) есть множество позиций j таких, что существует некоторая строка ... cd ..., входящая в язык, описываемый регулярным выражением, такая, что позиция i соответствует этому вхождению c, а позиция j - вхождению d.

Рис. 3.11.

Рис. 3.12.

Рис. 3.13.
Рассмотрим теперь алгоритм построения ДКА с минимальным числом состояний, эквивалентного данному ДКА [?].
Пусть M = (Q, T, D, q0, F) - ДКА. Будем называть M всюду определенным, если D(q, a)




Лемма. Пусть M = (Q, T, D, q0, F) - ДКА, не являющийся всюду определенным. Существует всюду определенный ДКА M', такой что L(M) = L(M').
Доказательство. Рассмотрим автомат

где q'

(1) Для всех




(2) Для всех



(3) Для всех

Легко показать, что автомат M' допускает тот же язык, что и M.
Приведенный ниже алгоритм получает на входе всюду определенный автомат. Если автомат не является всюду определенным, его можно сделать таковым на основании только что приведенной леммы.
Алгоритм 3.4. Построение ДКА с минимальным числом состояний.
Вход. Всюду определенный ДКА M = (Q, T, D, q0, F).
Выход. ДКА

Метод. Выполнить шаги 1-5:
(1) Построить начальное разбиение ? множества состояний из двух групп: заключительные состояния Q и остальные Q - F, то есть ? = {F, Q - F}.
(2) Применить к ? следующую процедуру и получить новое разбиение ?new:
for (каждой группы G в ?){ разбить G на подгруппы так, чтобы состояния s и t из G оказались в одной подгруппе тогда и только тогда, когда для каждого входного символа a состояния s и t имеют переходы по a в состояния из одной и той же группы в ?, заменить G в ?new на множество всех полученных подгрупп, }
(3) Если ?new = ?, полагаем ?res = ? и переходим к шагу 4, иначе повторяем шаг 2 с ? := ?new.
(4)

Таким образом, каждая группа в ?res становится состоянием нового автомата M'. Если группа содержит начальное состояние автомата M, то эта группа становится начальным состоянием автомата M'. Если группа содержит заключительное состояние M, она становится заключительным состоянием M'. Отметим, что каждая группа ?res либо состоит только из состояний из F, либо не имеет состояний из F. Переходы определяются очевидным образом.
(5) Если M' имеет "мертвое"состояние, то есть состояние, которое не является допускающим и из которого нет путей в допускающие, удалить его и связанные с ним переходы из M'. Удалить из M' также все состояния, недостижимые из начального.
Пример 3.10. Результат применения алгоритма 3.4 приведен на рис. 3.15.

Рис. 3.15.
Построение недетерминированного конечного автомата по регулярному выражению
Рассмотрим алгоритм построения по регулярному выражению недетерминированного конечного автомата, допускающего тот же язык.
Алгоритм 3.1. Построение недетерминированного конечного автомата по регулярному выражению.
Вход. Регулярное выражение r в алфавите T.
Выход. НКА M, такой что L(M) = L(r).
Метод. Автомат для выражения строится композицией из автоматов, соответствующих подвыражениям. На каждом шаге построения строящийся автомат имеет в точности одно заключительное состояние, в начальное состояние нет переходов из других состояний и нет переходов из заключительного состояния в другие.
Для выражения e строится автомат

Рис. 3.5.
Для выражения


Рис. 3.6.
Для выражения s|t автомат M(s|t) строится как показано на рис. 3.7. Здесь i - новое начальное состояние и f - новое заключительное состояние. Заметим, что имеет место переход по e из i в начальные состояния M(s) и M(t) и переход по e из заключительных состояний M(s) и M(t) в f. Начальное и заключительное состояния автоматов M(s) и M(t) не являются таковыми для автомата M(s|t).

Рис. 3.7.
Для выражения st автомат M(st) строится следующим образом:

Рис. 3.8.
Начальное состояние автомата M(s) становится начальным для нового автомата, а заключительное состояние M(t) становится заключительным для нового автомата. Начальное состояние M(t) и заключительное состояние M(s) сливаются, то есть все переходы из начального состояния M(t) становятся переходами из заключительного состояния M(s). В новом автомате это объединенное состояние не является ни начальным, ни заключительным. Для выражения s* автомат M(s*) строится следующим образом:
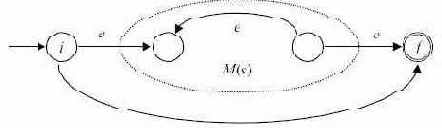
Рис. 3.9.
Здесь i - новое начальное состояние, а f - новое заключительное состояние.
Программирование лексического анализа
Как уже отмечалось ранее, лексический анализатор (ЛА) может быть оформлен как подпрограмма. При обращении к ЛА, вырабатываются как минимум два результата: тип выбранной лексемы и ее значение (если оно есть).
Если ЛА сам формирует таблицы объектов, он выдает тип лексемы и указатель на соответствующий вход в таблице объектов. Если же ЛА не работает с таблицами объектов, он выдает тип лексемы, а ее значение передается, например, через некоторую глобальную переменную. Помимо значения лексемы, эта глобальная переменная может содержать некоторую дополнительную информацию: номер текущей строки, номер символа в строке и т.д. Эта информация может использоваться в различных целях, например, для диагностики.
В основе ЛА лежит диаграмма переходов соответствующего конечного автомата. Отдельная проблема здесь - анализ ключевых слов. Как правило, ключевые слова - это выделенные идентификаторы. Поэтому возможны два основных способа распознавания ключевых слов: либо очередная лексема сначала диагностируется на совпадение с каким-либо ключевым словом и в случае неуспеха делается попытка выделить лексему из какого-либо класса, либо, наоборот, после выборки лексемы идентификатора происходит обращение к таблице ключевых слов на предмет сравнения. Подробнее о механизмах поиска в таблицах будет сказано ниже (гл. "Организация таблиц символов "), здесь отметим только, что поиск ключевых слов может вестись либо в основной таблице имен и в этом случае в нее до начала работы ЛА загружаются ключевые слова, либо в отдельной таблице. При первом способе все ключевые слова непосредственно встраиваются в конечный автомат ЛА, во втором конечный автомат содержит только разбор идентификаторов.
В некоторых языках (например, ПЛ/1 или Фортран) ключевые слова могут использоваться в качестве обычных идентификаторов. В этом случае работа ЛА не может идти независимо от работы синтаксического анализатора. В Фортране возможны, например, следующие строки:
DO 10 I=1,25 DO 10 I=1.25
В первом случае строка - это заголовок цикла DO, во втором - оператор присваивания.
Поэтому, прежде чем можно будет выделить лексему, ЛА должен заглянуть довольно далеко. Еще сложнее дело в ПЛ/1. Здесь возможны такие операторы:
IF ELSE THEN ELSE = THEN, ELSE THEN = ELSE,
или
DECLARE (A1, A2, ... , AN)
и только в зависимости от того, что стоит после ")", можно определить, является ли DECLARE ключевым словом или идентификатором. Длина такой строки может быть сколь угодно большой и уже невозможно отделить фазу синтаксического анализа от фазы лексического анализа.
Рассмотрим несколько подробнее вопросы программирования ЛА. Основная операция ЛА, на которую уходит большая часть времени его работы - это взятие очередного символа и проверка на принадлежность его некоторому диапазону. Например, основной цикл при выборке числа в простейшем случае может выглядеть следующим образом:
while (Insym <='9' && Insym>='0') { ... }
Программу можно значительно улучшить следующим образом [5]. Пусть LETTER, DIGIT, BLANK - элементы перечислимого типа. Введем массив map, входами которого будут символы, значениями - типы символов. Инициализируем массив map следующим образом:
map['a']=LETTER, ........ map['z']=LETTER, map['0']=DIGIT, ........ map['9']=DIGIT, map[' ']=BLANK, ........
Тогда приведенный цикл примет следующую форму:
while (map[Insym]==DIGIT) { ... }
Выделение ключевых слов может осуществляться после выделения идентификаторов. ЛА работает быстрее, если ключевые слова выделяются непосредственно.
Для этого строится конечный автомат, описывающий множество ключевых слов. На рис. 3.17 приведен фрагмент такого автомата.
Рассмотрим пример программирования этого конечного автомата на языке Си, приведенный в [17]:

Рис. 3.17.
........ case 'i': if (cp[0]=='f' &&!(map[cp[2]] & (DIGIT | LETTER))) {cp++, return IF,} if (cp[0]=='n' && cp[1]=='t' &&!(map[cp] & (DIGIT | LETTER))) {cp+=2, return INT,} { обработка идентификатора } ........
Здесь cp - указатель текущего символа. В массиве map классы символов кодируются битами.
Поскольку ЛА анализирует каждый символ входного потока, его скорость существенно зависит от скорости выборки очередного символа входного потока. В свою очередь, эта скорость во многом определяется схемой буферизации. Рассмотрим возможные эффективные схемы буферизации.

Рис. 3.18.
Будем использовать буфер, состоящий из двух одинаковых частей длины N (рис. 3.18, а), где N - размер блока обмена (например, 1024, 2048 и т.д.). Чтобы не читать каждый символ отдельно, в каждую из половин буфера поочередно одной командой чтения считывается N символов. Если на входе осталось меньше N символов, в буфер помещается специальный символ (eof). На буфер указывают два указателя: продвижение и начало. Между указателями размещается текущая лексема. Вначале они оба указывают на первый символ выделяемой лексемы. Один из них, продвижение, продвигается вперед, пока не будет выделена лексема, и устанавливается на ее конец. После обработки лексемы оба указателя устанавливаются на символ, следующий за лексемой. Если указатель продвижение переходит середину буфера, правая половина заполняется новыми N символами. Если указатель продвижение переходит правую границу буфера, левая половина заполняется N символами и указатель продвижение устанавливается на начало буфера.
При каждом продвижении указателя необходимо проверять, не достигли ли мы границы одной из половин буфера. Для всех символов, кроме лежащих в конце половин буфера, требуются две проверки. Число проверок можно свести к одной, если в конце каждой половины поместить дополнительный _сторожевойї символ, в качестве которого логично взять eof (рис. 3.18, б).
В этом случае почти для всех символов делается единственная проверка на совпадение с eof и только в случае совпадения нужно дополнительно проверить, достигли ли мы середины или правого конца.
Регулярные множества и выражения
Введем понятие регулярного множества, играющего важную роль в теории формальных языков.
Регулярное множество в алфавите T определяется рекурсивно следующим образом:





ничто другое не является регулярным множеством в алфавите T.
Итак, множество в алфавите T регулярно тогда и только тогда, когда оно либо


Приведенное выше определение регулярного множества позволяет ввести следующую удобную форму его записи, называемую регулярным выражением.
Регулярное выражение в алфавите T и обозначаемое им регулярное множество в алфавите T определяются рекурсивно следующим образом:


(p|q) - регулярное выражение, обозначающее регулярное множество

ничто другое не является регулярным выражением в алфавите T.
Мы будем опускать лишние скобки в регулярных выражениях, договорившись о том, что операция итерации имеет наивысший приоритет, затем идет операции конкатенации, наконец, операция объединения имеет наименьший приоритет.
Кроме того, мы будем пользоваться записью p+ для обозначения pp*. Таким образом, запись (a|((ba)(a*))) эквивалентна a|ba+.
Также, мы будем использовать запись L(r) для регулярного множества, обозначаемого регулярным выражением r.
Пример 3.1. Несколько примеров регулярных выражений и обозначаемых ими регулярных множеств:
a(e|a)|b - обозначает множество {a; b; aa};a(a|b)* - обозначает множество всевозможных цепочек, состоящих из a и b, начинающихся с a;(a|b)*(a|b)(a|b)* - обозначает множество всех непустых цепочек, состоящих из a и b, то есть множество {a, b}+;((0|1)(0|1)(0|1))* - обозначает множество всех цепочек, состоящих из нулей и единиц, длины которых делятся на 3.
Ясно, что для каждого регулярного множества можно найти регулярное выражение, обозначающее это множество, и наоборот. Более того, для каждого регулярного множества существует бесконечно много обозначающих его регулярных выражений.
Будем говорить, что регулярные выражения равны или эквивалентны (=), если они обозначают одно и то же регулярное множество.
Существуют алгебраические законы, позволяющие осуществлять эквивалентное преобразование регулярных выражений.
Лемма. Пусть p, q и r - регулярные выражения. Тогда справедливы следующие соотношения:
p|q = q|p;





Следствие. Для любого регулярного выражения существует эквивалентное регулярное выражение, которое либо есть


В дальнейшем будем рассматривать только регулярные выражения, не содержащие в своей записи


где di - различные имена, а каждое ri - регулярное выражение над символами

можно построить регулярное выражение над T, повторно заменяя имена регулярных выражений на обозначаемые ими регулярные выражения.
Пример 3.2. Несколько примеров использования имен для обозначения регулярных выражений.
Регулярное выражение для множества идентификаторов.

Регулярное выражение для множества чисел в десятичной записи.

Связь регулярных множеств, конечных автоматов и регулярных грамматик
В разделе 3.3.3 приведен алгоритм построения детерминированного конечного автомата по регулярному выражению. Рассмотрим теперь как по описанию конечного автомата построить регулярное множество, совпадающее с языком, допускаемым конечным автоматом.
Теорема 3.1. Язык, допускаемый детерминированным конечным автоматом, является регулярным множеством.
Доказательство. Пусть L - язык, допускаемый детерминированным конечным автоматом

Введем De - расширенную функцию переходов автомата M: De(q, w) = p, где


Обозначим посредством


Иными словами,



Таким образом, определение

Цепочка w принадлежит




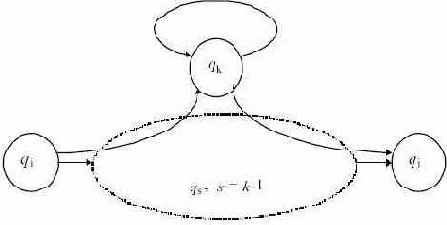
Рис. 3.16.
Тогда

Таким образом, для всякого регулярного множества имеется конечный автомат, допускающий в точности это регулярное множество, и наоборот - язык, допускаемый конечным автоматом есть регулярное множество.
Рассмотрим теперь соотношение между языками, порождаемыми праволинейными грамматиками и допускаемыми конечными автоматами.
Праволинейная грамматика G = (N, T, P, S) называется регулярной, если
(1) каждое ее правило, кроме S




(2) в том случае, когда

Лемма. Пусть G - праволинейная грамматика. Существует регулярная грамматика G' такая, что L(G) = L(G').
Доказательство. Предоставляется читателю в качестве упражнения.
Теорема 3.2. Пусть G = (N, T, P, S) - праволинейная грамматика. Тогда существует конечный автомат M = (Q, T, D, q0, F) для которого L(M) = L(G).
Доказательство. На основании приведенной выше леммы, без ограничения общности можно считать, что G - регулярная грамматика.
Построим НКА M следующим образом:
состояниями M будут нетерминалы G плюс новое состояние R, не принадлежащее N. Так что








M, читая вход w, моделирует вывод w в грамматике G. Покажем, что L(M) = L(G). Пусть






Аналогично, если







Теорема 3.3. Для каждого конечного автомата M = (Q, T, D, q0, F) существует праволинейная грамматика G = (N, T, P, S) такая, что L(G) = L(M).
Доказательство. Без потери общности можно считать, что автомат M - детерминированный. Определим грамматику G следующим образом:
нетерминалами грамматики G будут состояния автомата M. Так что N = Q,в качестве начального символа грамматики G примем q0, то есть S = q0,





Доказательство того, что


В некоторых случаях для определения того, является ли язык регулярным, может быть полезным необходимое условие, которое называется леммой Огдена о разрастании.
Теорема 3.4. (Лемма о разрастании для регулярных множеств). Пусть L - регулярное множество. Существует такая константа k, что если

и




Доказательство. Пусть M = (Q, ?, D, q0, F) - конечный автомат, допускающий L, то есть L(M) = L и k = |Q|. Пусть



для некоторых






С помощью леммы о разрастании можно показать, что не является регулярным множеством язык L={0n1n|n

Допустим, что L регулярен. Тогда для достаточно большого n0n1n можно представить в виде xyz, причем y








Алгоритм Кока-Янгера-Касами
Приведем алгоритм синтаксического анализа, применимый для любой грамматики в нормальной форме Хомского
Алгоритм Кока-Янгера-Касами
Вход. КС-грамматика G = (N, T, P, S) в нормальной форме Хомского и входная цепочка

Выход. Таблица разбора Tab для w такая, что


Метод.
(1) Положить



(2) Пусть tij вычислено для 1





Так как 1





(3) Повторять шаг 2 до тех пор, пока не станут известны tij
для всех 1




Алгоритм нахождения левого разбора по таблице разбора Tab.
Вход. КС-грамматика G = (N, T, P, S) в нормальной форме Хомского с правилами, занумерованными от 1 до p, входная цепочка

Выход. Левый разбор цепочки w или сигнал ошибка.
Метод. Процедура gen(i, j, A):
(1) Если j = 1 и A

(2) Пусть j > 1 и k - наименьшее из чисел от 1 до j-1, для которых существует


Выполнить gen(1, n, S), если

Алгоритм разбора сверху-вниз
Пусть дана КС-грамматика G = (N; T; P; S). Рассмотрим разбор сверху-вниз (предсказывающий разбор) для грамматики G.
Главная задача предсказывающего разбора - определение правила вывода, которое нужно применить к нетерминалу. Процесс предсказывающего разбора с точки зрения построения дерева разбора проиллюстрирован на рис. 4.1
Фрагменты недостроенного дерева соответствуют сентенциальным формам. Вначале дерево состоит только из одной вершины, соответствующей аксиоме S. В этот момент по первому символу входной цепочки предсказывающий анализатор должен определить правило S


На рис. 4.2 условно показана структура предсказывающего анализатора, который определяет
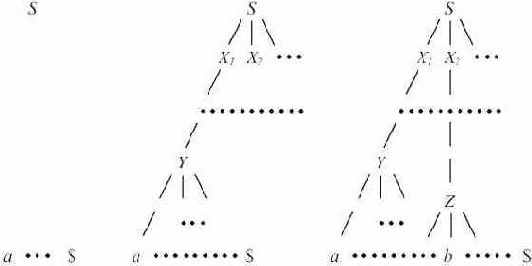
Рис. 4.1.
очередное правило с помощью таблицы. Такую таблицу можно построить и непосредственно по грамматике. Таблично-управляемый предсказывающий анализатор имеет входную ленту, управляющее устройство (программу), таблицу анализа, магазин (стек) и выходную ленту. Входная лента содержит анализируемую строку, заканчивающуюся символом $ - маркером конца строки. Выходная лента содержит последовательность примененных правил вывода.

Рис. 4.2.
Таблица анализа - это двумерный массив M[A; a], где A - нетерминал, и a - терминал или символ $. Значением M[A; a] может быть некоторое правило грамматики или элемент "ошибка".
Магазин может содержать последовательность символов грамматики с $ на дне. В начальный момент магазин содержит только начальный символ грамматики на верхушке и $ на дне.
Анализатор работает следующим образом. Вначале анализатор находится в конфигурации, в которой магазин содержит S$, на входной ленте w$ (w - анализируемая цепочка), выходная лента пуста.
На каждом такте анализатор рассматривает X - символ на верхушке магазина и a - текущий входной символ. Эти два символа определяют действия анализатора. Имеются следующие возможности.
Если X=a=$, анализатор останавливается, сообщает об успешном окончании разбора и выдает содержимое выходной ленты.Если X= a


Поместить '$', затем S в магазин; do {X=верхний символ магазина; if (X - терминал) if (X==InSym) {удалить X из магазина; InSym=очередной символ; } else {error(); break;} else if (X - нетерминал) if (M[X,InSym]=="X->Y1Y2...Yk") {удалить X из магазина; поместить Yk,Yk-1,...Y1 в магазин (Y1 на верхушку); вывести правило X->Y1Y2...Yk; } else {error(); break;} /*вход таблицы M пуст*/ } while (X!='$'); /*магазин пуст*/ if (InSym != '$') error(); /*Не вся строка прочитана*/
Пример 4.3. Рассмотрим грамматику арифметических выражений G=({E; E', T, T', F}, {id, +, *, (, )}, P, E) с правилами:

В таблица 4.3 приведена предсказывающего анализатора для этой грамматики. Пустые клетки таблицы соответствуют элементу "ошибка".
| Нетерминал | Входной символ | |||||
| id | + | * | ( | ) | $ | |
| E | E | E | ||||
| E' | E' | E' | E' | |||
| T | T | T | ||||
| T' | T' | T' | T' | T' | ||
| F | F | F | ||||
При разборе входной цепочки id + id * id$ анализатор совершает последовательность шагов, изображенную в таблица 4.4.
Заметим, что анализатор осуществляет в точности левый вывод. Если за уже просмотренными входными символами поместить символы грамматики в магазине, то можно получить в точности левые сентенциальные формы вывода. Дерево разбора для этой цепочки приведено на рис. рис. 4.3.
| Магазин | Вход | Выход |
| E$ | id + id * id$ | |
| TE'$ | id + id * id$ | E  |
| FT'E'$ | id + id * id$ | T  |
| id T'E'$ | id + id * id$ | F  |
| T'E'$ | +id * id$ | |
| E'$ | +id * id$ | T'  |
| +TE'$ | +id * id$ | E'  |
| TE'$ | id * id$ | |
| FT'E'$ | id * id$ | T  |
| id T'E'$ | id * id$ | F  |
| T'E'$ | *id$ | |
| *F'T'E'$ | *id$ | T'  |
| FT'E'$ | id$ | |
| id T'E'$ | id$ | F  |
| T'E'$ | $ | |
| E'$ | $ | T'  |
| $ | $ | E'  |
Функции FIRST и FOLLOW
При построении таблицы предсказывающего анализатора нам потребуются две функции - FIRST и FOLLOW.
Пусть G = (N, T, P, S) - КС-грамматика. Для



Рис. 4.3.
начинаются строки, выводимые из




Определим FOLLOW(A) для нетерминала A как множество терминалов a, которые могут появиться непосредственно справа от A в некоторой сентенциальной форме грамматики, то есть множество терминалов a таких, что существует вывод вида S



Рассмотрим алгоритмы вычисления функции FIRST.
Алгоритм 4.3. Вычисление FIRST для символов КС- грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FIRST(X) для каждого символа

Метод. Выполнить шаги 1-3:
(1) Если X - терминал, то положить FIRST(X) = {X}; если X - нетерминал, положить FIRST(X) =

(2) Если в P имеется правило X

(3) Пока ни к какому множеству FIRST(X) нельзя уже будет добавить новые элементы, выполнять:
do { continue = false; Для каждого нетерминала X Для каждого правила X



Конструирование LR(1)-таблицы
Рассмотрим алгоритм конструирования таблицы, управляющей LR(1) - анализатором.
Пусть G = (N, T, P, S) - КС-грамматика. Пополненной грамматикой для данной грамматики G называется КС- Состояния Action Goto

Рис. 4.7.

Рис. 4.8.
грамматика

то есть эквивалентная грамматика, в которой введен новый начальный символ S' и новое правило вывода S'

Это дополнительное правило вводится для того, чтобы определить, когда анализатор должен остановить разбор и зафиксировать допуск входа. Таким образом, допуск имеет место тогда и только тогда, когда анализатор готов осуществить свертку по правилу S'

LR(1)-ситуацией называется пара [A




Будем говорить, что LR(1)-ситуация [A




Будем говорить, что ситуация допустима, если она допустима для какого-либо активного префикса.
Пример 4.11. Дана грамматика G = ({S, B}, {a, b}, P, S) с правилами
S

B

Существует правосторонний вывод





Центральная идея метода заключается в том, что по грамматике строится детерминированный конечный автомат, распознающий активные префиксы. Для этого ситуации группируются во множества, которые и образуют состояния автомата. Ситуации можно рассматривать как состояния недетерминированного конечного автомата, распознающего активные префиксы, а их группировка на самом деле есть процесс построения детерминированного конечного автомата из недетерминированного.
Анализатор, работающий слева-направо по типу сдвиг- свертка, должен уметь распознавать основы на верхушке магазина. Состояние автомата после прочтения содержимого магазина и текущий входной символ определяют очередное действие автомата.
Функцией переходов этого конечного автомата является функция переходов LR-анализатора.
Чтобы не просматривать магазин на каждом шаге анализа, на верхушке магазина всегда хранится то состояние, в котором должен оказаться этот конечный автомат после того, как он прочитал символы грамматики в магазине от дна к верхушке. Рассмотрим ситуацию вида [A










Система множеств допустимых LR(1)-ситуаций для всевозможных активных префиксов пополненной грамматики называется канонической системой множеств допустимых LR(1)-ситуаций. Алгоритм построения канонической системы множеств приведен ниже.
Алгоритм 4.10. Конструирование канонической системы множеств допустимых LR(1)-ситуаций.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Каноническая система C множеств допустимых LR(1)-ситуаций для грамматики G.
Метод. Выполнить для пополненной грамматики G' процедуру items, которая использует функции closure и goto.
function closure(I){ /* I - множество ситуаций */ do{ for (каждой ситуации [A





function goto(I,X){ /* I - множество ситуаций; X - символ грамматики */ Пусть J = {[A




procedure items(G'){ /* G' - пополненная грамматика */ I' = closure({[S'

Если I - множество ситуаций, допустимых для некоторого активного префикса +, то goto(I, X) - множество ситуаций, допустимых для активного префикса +X.
Работа алгоритма построения системы C множеств допустимых LR(1)-ситуаций начинается с того, что в C помещается начальное множество ситуаций I0 = closure({[S'

По-существу, goto(I, X) - переход конечного автомата из состояния I по символу X.
Рассмотрим теперь, как по системе множеств LR(1)-ситу- аций строится LR(1)-таблица, то есть функции действий и переходов LR(1)-анализатора.
Алгоритм 4.11. Построение LR(1)-таблицы.
Вход. Каноническая система C = {I0, I1, ... , In} множеств допустимых LR(1)-ситуаций для грамматики G.
Выход. Функции Action и Goto, составляющие LR(1)- таблицу для грамматики G.
Метод. Для каждого состояния i функции Action[i, a] и Goto[i, X] строятся по множеству ситуаций Ii:
Значения функции действия (Action) для состояния i определяются следующим образом:
если






Значения функции переходов для состояния i определяются следующим образом: если goto(Ii, A) = Ij , то Goto[i, A] = j (здесь A - нетерминал). Все входы в Action и Goto, не определенные шагами 2 и 3, полагаем равными error. Начальное состояние анализатора строится из множества, содержащего ситуацию [S'

Таблица на основе функций Action и Goto, полученных в результате работы алгоритма 4.11., называется канонической LR(1)-таблицей. Работающий с ней LR(1)-анализатор, называется каноническим LR(1)-анализатором.
Пример 4.12. Рассмотрим следующую грамматику, являющуюся пополненной для грамматики из примера 4.8.:
(0) E'

(1) E

(2) E

(3) T

(4) T

(5) F

Множества ситуаций и переходы по goto для этой грамматики приведены на рис. 4.9. LR(1)-таблица для этой грамматики приведена на рис. 4.7.
Проследим последовательность создания этих множеств более подробно.
Вычисляем I0 = closure({[E'



Значит, для терминала $ добавляем ситуации на основе правил со знаком E в левой части правила. Это правила

и соответствующие им ситуации

Просматриваем получившиеся ситуации. Для ситуации [E

[E



[T



[T




увеличить изображение
Рис. 4.9.
[T








Таким образом, все 14 искомых ситуаций I0 получены.
Возвращаемся в головную функцию items, включаем I0 в множество C и исследуем непустые итоги применения функции goto(I0; X), где

Если посмотреть на вид правил в функции goto(I0; X), то видно, что X должен встретиться в правой части хотя бы одного правила. Для E0 таких правил у нас нет, поэтому значение функции goto(I0, E') пусто.
Возьм_м goto(I0; E). E встречается после точки в правых частях двух ситуаций из I0, значит бер_м эти два правила и переносим в них точки на один символ вправо (пока есть куда - не уперлись в запятую), получаем:
[E'

и
[E

Вычислим от каждой из этих ситуаций функцию closure. Но, поскольку справа от точки здесь либо пустая цепочка, либо терминал, то никаких новых ситуаций не возникает. Дальше отслеживаем, может ли куда-то сдвинуться точка дальше на право и по какому символу. Если может, строим соответствующее множество (рис. 4.9). И т.д.
Конструирование таблицы предсказывающего анализатора
Для конструирования таблицы предсказывающего анализатора по грамматике G может быть использован алгоритм, основанный на следующей идее. Предположим, что A








Алгоритм 4.7. Построение таблицы предсказывающего анализатора.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Таблица M[A; a] предсказывающего анализатора,

Метод. Для каждого правила вывода A


(1) Для каждого терминала a из FIRST(R) добавить A

(2) Если






(3) Положить все неопределенные входы равными "ошибка".
Пример 4.5. Применим алгоритм 4.7 к грамматике из примера 4.3. Поскольку FIRST(TE') = FIRST(T) = {(, id }, в соответствии с правилом вывода E


В соответствии с правилом вывода E'




Таблица анализа, построенная по алгоритму 4.7. для этой грамматики, приведена в таблица 4.3.
Контекстно-свободные грамматики и автоматы с магазинной памятью
Пусть G = (N, T, P, S) - КС-грамматика. Введем несколько важных понятий и определений.
Вывод, в котором в любой сентенциальной форме на каждом шаге делается подстановка самого левого нетерминала, называется левосторонним. Если S



Упорядоченным графом называется пара (V,E), где V есть множество вершин, а E - множество линейно упорядоченных списков дуг, каждый элемент которого имеет вид ((v, v1), (v, v2), ... , (v, vn)). Этот элемент указывает, что из вершины v выходят n дуг, причем первой из них считается дуга, входящая в вершину v1, второй - дуга, входящая в вершинуv2, и т.д.
Упорядоченным помеченным деревом называется упорядоченный граф (V,E), основой которого является дерево и для которого определена функция f : V

Упорядоченное помеченное дерево D называется деревом вывода (или деревом разбора) цепочки w в КС-грамматике G = (N, T, P, S), если выполнены следующие условия:
(1) корень дерева D помечен S;
(2) каждый лист помечен либо

(3) каждая внутренняя вершина помечена нетерминалом

(4) если X - нетерминал, которым помечена внутренняя вершина и X1, ... , Xn - метки ее прямых потомков в указанном порядке, то X

(5) Цепочка, составленная из выписанных слева направо меток листьев, равна w.
Процесс определения принадлежности данной строки языку, порождаемому данной грамматикой, и, в случае указанной принадлежности, построение дерева разбора для этой строки, называется синтаксическим анализом. Можно говорить о восстановлении дерева вывода (в частности, правостороннего или левостороннего) для строки, принадлежащей языку. По восстановленному выводу можно строить дерево разбора.
Грамматика G называется неоднозначной, если существует цепочка w, для которой имеется два или более различных деревьев вывода в G.
Грамматика G называется леворекурсивной, если в ней имеется нетерминал A такой, что для некоторой цепочки R существует вывод A


Автомат с магазинной памятью (МП-автомат) - это семерка M = (Q, T, ?, D, q0, Z0, F), где
(1) Q - конечное множество состояний, представляющих всевозможные состояния управляющего устройства;
(2) T - конечный входной алфавит;
(3) ? - конечный алфавит магазинных символов;
(4) D - отображение множества Q x (T

(5)

(6)

(7)

Конфигурация МП-автомата - это тройка (q, w, u), где
(1)

(2)

(3)

Такт работы МП-автомата M будем представлять в виде бинарного отношения

Будем писать

если множество D(q, a, Z) содержит (p, v), где


Начальной конфигурацией МП-автомата M называется конфигурация вида (q0, w, Z0), где

>Заключительной конфигурацией называется конфигурация вида (q, e, u), где

Введем транзитивное и рефлексивно-транзитивное замыкание отношения




Говорят, что цепочка w допускается МП-автоматом M, если



Множество всех цепочек, допускаемых автоматом M называется языком, допускаемым (распознаваемым, определяемым) автоматом M (обозначается L(M)).
Пример 4.1. Рассмотрим МП-автомат
M = ({q0, q1, q2}, {a, b}, {Z, a, b}, D, q0, Z, {q2}),
у которого функция переходов D содержит элементы:
D(q0, a, Z) = {(q0, aZ)}, D(q0, b, Z) = {(q0, bZ)}, D(q0, a, a) = {(q0, aa), {q1, e)}, D(q0, a, b) = {(q0, ab)}, D(q0, b, a) = {(q0, ba)}, D(q0, b, b) = {(q0, bb), (q1, e)}, D(q1, a, a) = {(q1, e)}, D(q1, b, b) = {(q1, e)}, D(q1, e, Z) = {(q2, e)}.
Нетрудно показать, что

Иногда допустимость определяют несколько иначе: цепочка w допускается МП-автоматом M, если


Левая факторизация
Oсновная идея левой факторизации в том, что в том случае, когда неясно, какую из двух альтернатив надо использовать для развертки нетерминала A, нужно изменить A-правила так, чтобы отложить решение до тех пор, пока не будет достаточно информации для принятия правильного решения.
Если A









A


A'

Алгоритм 4.9. Левая факторизация грамматики.
Вход. КС-грамматика G.
Выход. Левофакторизованная КС-грамматика G', эквивалентная G.
Метод. Для каждого нетерминала A найти самый длинный префикс



A




где z обозначает все альтернативы, не начинающиеся с

A


A'

где A' - новый нетерминал. Применять это преобразование, пока никакие две альтернативы не будут иметь общего префикса.
Пример 4.9. Рассмотрим вновь грамматику условных операторов из примера 4.6:
S


После левой факторизации грамматика принимает вид
S



К сожалению, грамматика остается неоднозначной, а значит, и не LL(1)-грамматикой.
LL(1)-грамматики
Алгоритм 4.7 построения таблицы предсказывающего анализатора может быть применен к любой КС-грамматике. Однако для некоторых грамматик построенная таблица может иметь неоднозначно определенные входы. Например, нетрудно доказать, что если грамматика леворекурсивна или неоднозначна, таблица будет иметь по крайней мере один неоднозначно определенный вход.
Грамматики, для которых таблица предсказывающего анализатора не имеет неоднозначно определенных входов, называются LL(1)-грамматиками. Предсказывающий анализатор, построенный для LL(1)-грамматики, называется LL(1)-анализатором. Первая буква L в названии связано с тем, что входная цепочка читается слева направо, вторая L означает, что строится левый вывод входной цепочки, 1 - что на каждом шаге для принятия решения используется один символ непрочитанной части входной цепочки.
Доказано, что алгоритм 4.7 для каждой из LL(1)-грам- матик G строит таблицу предсказывающего анализатора, распознающего все цепочки из L(G) и только эти цепочки. Нетрудно доказать также, что если G - LL(1)-грамматика, то L(G) - детерминированный КС-язык.
Справедлив также следующий критерий LL(1)-граммати- ки. Грамматика G = (N, T, P, S) является LL(1)-грамматикой тогда и только тогда, когда для каждой пары правил A



(то есть правил с одинаковой левой частью) выполняются следующие 2 условия:
(1)

(2) Если



Язык, для которого существует порождающая LL(1)- грамматика, называют LL(1)-языком. Доказано, что проблема определения, порождает ли грамматика LL-язык, является алгоритмически неразрешимой.
Пример 4.6. Неоднозначная грамматика не является LL(1). Примером может служить следующая грамматика
G = ({S, E}, {if, then, else, a, b}, P, S) с правилами: S


Эта грамматика является неоднозначной, что иллюстрируется на рис. 4.4.
LL(k)-грамматики
Определение. КС-грамматика G = (N, ?, P, S) называется LL(k)-грамматикой для некоторого фиксированного k, если из
(1)

(2)

и
FIRSTk(x) = FIRSTk(y), вытекает, что ? = ?.
Говоря менее формально, G будет LL(k)- грамматикой, если для данной цепочки



Рис. 4.4.
начинающейся с ? и продолжающейся упомянутыми k терминалами.
Грамматика называется LL(k)-грамматикой, если она LL(k)-грамматика для некоторого k.
Пример 4.7. Рассмотрим грамматику G = ({S, A, B}, {0, 1, a, b}, P, S), где P состоит из правил
S



Здесь L(G) = an0bn | n





Обращаясь к точному определению LL(k)-грамматики, положим ? =


соответствуют выводам (1) и (2) определения. Первые k символов цепочек x и y совпадают. Однако заключение ? = ? ложно. Так как k здесь выбрано произвольно, то G не является LL-грамматикой.
LR(1)-анализаторы
В названии LR(1) символ L указывает на то, что входная цепочка читается слева-направо, R - на то, что строится правый вывод, наконец, 1 указывает на то, что анализатор видит один символ непрочитанной части входной цепочки.
LR(1)-анализ привлекателен по нескольким причинам:
LR(1)-анализ - наиболее мощный метод анализа без возвратов типа сдвиг-свертка;LR(1)-анализ может быть реализован довольно эффективно;LR(1)-анализаторы могут быть построены для практически всех конструкций языков программирования;класс грамматик, которые могут быть проанализированы LR(1)-методом, строго включает класс грамматик, которые могут быть проанализированы предсказывающими анализаторами (сверху-вниз типа LL(1)).
Схематически структура LR(1)-анализатора изображена на рис. 4.4. Анализатор состоит из входной ленты, выходной ленты, магазина, управляющей программы и таблицы анализа (LR(1)-таблицы), которая имеет две части - функцию действий (Action) и функцию переходов (Goto). Управляющая программа одна и та же для всех LR(1)-анализаторов, разные анализаторы отличаются только таблицами анализа.
Анализатор читает символы на входной ленте по одному за шаг. В процессе анализа используется магазин, в котором хранятся строки вида S0X1S1X2S2 ... XmSm (Sm - верхушка магазина). Каждый Xi - символ грамматики (терминальный или нетерминальный), а Si - символ состояния.
Заметим, что символы грамматики (либо символы состояний) не обязательно должны размещаться в магазине. Однако, их использование облегчает понимание поведения LR-анализатора.
Элемент функции действий Action[Sm; ai] для символа состояния Sm и входа

shift S (сдвиг), где S - символ состояния,reduce A


Элемент функции переходов Goto[Sm; A] для символа состояния Smи входа


Рис. 4.6.
S, где S - символ состояния,error (ошибка).
Конфигурацией LR(1)-анализатора называется пара, первая компонента которой - содержимое магазина, а вторая - непросмотренный вход:
(S0X1S1X2S2 ... XmSm, aiai+1 ... an$)
Эта конфигурация соответствует правой сентенциальной форме
X1X2 ... Xmaiai+1 ... an
Префиксы правых сентенциальных форм, которые могут появиться в магазине анализатора, называются активными префиксами. Основа сентенциальной формы всегда располагается на верхушке магазина. Таким образом, активный префикс - это такой префикс правой сентенциальной формы, который не переходит правую границу основы этой формы.
Когда анализатор начинает работу, в магазине находится только символ начального состояния S0, на входной ленте - анализируемая цепочка с маркером конца.
Каждый очередной шаг анализатора определяется текущим входным символом ai и символом состояния на верхушке магазина Sm следующим ниже образом.
Пусть LR(1)-анализатор находится в конфигурации
(S0X1S1X2S2 ... XmSm, aiai+1 ... an$)
Анализатор может проделать один из следующих шагов:
Если Action[Sm, ai] = shift S, то анализатор выполняет сдвиг, переходя в конфигурацию

и символ состояния S, определяемый Action[Sm, ai]. Текущим входным символом становится ai+1. Если Action[Sm, ai] = reduce A


Анализатор сначала удаляет из магазина 2r символов (r символов состояния и r символов грамматики), так что на верхушке оказывается состояние Sm-r. Затем анализатор помещает в магазин A - левую часть правила вывода, и S - символ состояния, определяемый Goto[Sm-r, A]. На шаге свертки текущий входной символ не меняется. Для LR(1)- анализаторов последовательность символов грамматики Xm-r+1 ... Xm, удаляемых из магазина , всегда соответствует ? - правой части правила вывода, по которому делается свертка.
После осуществления шага свертки генерируется выход LR(1)-анализатора, то есть исполняются семантические действия, связанные с правилом, по которому делается свертка, например, печатаются номера правил, по которым делается свертка.
Заметим, что функция Goto таблицы анализа, построенная по грамматике G, фактически представляет собой функцию переходов детерминированного конечного автомата, распознающего активные префиксы G. Если Action[Sm, ai] = accept, то разбор успешно завершен.Если Action[Sm, ai] = error, то анализатор обнаружил ошибку, и выполняются действия по диагностике и восстановлению.
Пример 4.10. Рассмотрим грамматику арифметических выражений G = ({E, T, F}, {id, +, *}, P, E) с правилами:
E





На рис. 4.7 изображены функции Action и Goto, образующие LR(1)-таблицу для этой грамматики. Элемент Si функции Action означает сдвиг и помещение в магазин состояния с номером i, Rj - свертку по правилу номер j, acc - допуск, пустая клетка - ошибку. Для функции Goto символ i означает помещение в магазин состояния с номером i, пустая клетка - ошибку.
На входе id + id * id последовательность состояний магазина и входной ленты показаны на рис. 4.8. Например, в первой строке LR-анализатор находится в нулевом состоянии и "видит" первый входной символ id. Действие S6 в нулевой строке и столбце id в поле Action (рис. 4.7) означает сдвиг и помещение символа состояния 6 на верхушку магазина. Это и изображено во второй строке: первый символ id и символ состояния 6 помещаются в магазин, а id удаляется со входной ленты.
Текущим входным символом становится +, и действием в состоянии 6 на вход + является свертка по F

LR(1)-грамматики
Если для КС-грамматики G функция Action, полученная в результате работы алгоритма 4.11., не содержит неоднозначно определ_нных входов, то грамматика называется LR(1)- грамматикой.
Язык L называется LR(1)-языком, если он может быть порожден некоторой LR(1)-грамматикой.
Иногда используется другое определение LR(1)-грамматики. Грамматика называется LR(1), если из условий


следует, что uAy = zBx (то есть u = z, A = B и x = y).
Согласно этому определению, если uvw и uvy - правовыводимые цепочки пополненной грамматики, у которых FIRST(w) = FIRST(y) и A


Можно доказать, что эти два определения эквивалентны. Дадим теперь определение LR(k)-грамматики.
Определение. Пусть G = (N, ?, P, S) - КС-грамматика и G' = (N', ?, P', S') - полученная из нее пополненная грамматика. Будем называть G LR(k)-грамматикой для k

(1)

(2)

(3)FIRSTk(w) = FIRSTk(y)
следует, что


Грамматика G называется LR-грамматикой, если она LR(k)-грамматика для некоторого k

Интуитивно это определение говорит о том, что если









Кроме того, работая с LR(k)-грамматикой, мы всегда знаем, допустить ли данную входную цепочку или продолжать разбор.
Пример 4.13. Рассмотрим грамматику G с правилами
S

Согласно определению, G не LR(0)-грамматика, так как из трeх условий
(1)


(3)FIRST0(e) = FIRST0(a) = e
не следует, что S'a = S: Применяя определение к этой ситуации, имеем

Пример 4.14. Пусть G - леволинейная грамматика с правилами

Заметим, что G не является LR(k)-грамматикой ни для какого k.
Допустим, что G - LR(k)-грамматика. Рассмотрим два правых вывода в пополненной грамматике G':

Эти два вывода удовлетворяют условию из определения LR(k)- грамматики при


Если грамматика не является LR(1), то анализатор типа сдвиг-свертка при анализе некоторой цепочки может достигнуть конфигурации, в которой он, зная содержимое магазина и следующий входной символ, не может решить, делать ли сдвиг или свертку (конфликт сдвиг/свертка), или не может решить, какую из нескольких сверток применить (конфликт свертка/свертка).
В частности, неоднозначная грамматика не может быть LR(1). Для доказательства рассмотрим два различных правых вывода
(1)

(2)

Нетрудно заметить, что LR(1) - условие (согласно второму определению LR(1)-грамматики) нарушается для наименьшего из чисел i, для которых un-i

Пример 4.15. Рассмотрим ещe раз грамматику условных операторов:

Если анализатор типа сдвиг-свертка находится в конфигурации, такой, что необработанная часть входной цепочки имеет вид else ... $, а в магазине находится ...
if E then S, то нельзя определить, является ли if E then S основой, вне зависимости от того, что лежит в магазине ниже. Это конфликт сдвиг/свертка. В зависимости от того, что следует на входе за else, правильной может быть свертка по S

Эта грамматика может быть преобразована к LR(1)-виду следующим образом:

Основная разница между LL(1)- и LR(1)- грамматиками заключается в следующем. Чтобы грамматика была LR(1)- грамматикой, необходимо распознавать вхождение правой части правила вывода, просмотрев все, что выведено из этой правой части и текущий символ входной цепочки. Это требование существенно менее строгое, чем требование для LL(1)-грамматики, когда необходимо определить применимое правило, видя только первый символ, выводимый из его правой части. Таким образом, класс LL(1)-грамматик есть собственный подкласс класса LR(1)-грамматик.
Справедливы также следующие утверждения [2].
Теорема 4.7. Каждый LR(1)-язык является детерминированным КС-языком.
Теорема 4.8. Если L - детерминированный КС-язык, то существует LR(1)-грамматика, порождающая L.
Теорема 4.9. Для любой LR(k)-грамматики для k > 1 существует эквивалентная ей LR(k \Gamma 1)-грамматика.
Доказано, что проблема определения, порождает ли грамматика LR-язык, является алгоритмически неразрешимой.
Основа
В процессе разбора снизу-вверх типа сдвиг-свертка строится дерево разбора входной цепочки, начиная с листьев (снизу) к корню (вверх). Этот процесс можно рассматривать как "свертку" цепочки w к начальному символу грамматики. На каждом шаге свертки подцепочка, которую можно сопоставить правой части некоторого правила вывода, заменяется символом левой части этого правила вывода, и если на каждом шаге выбирается правильная подцепочка, то в обратном порядке прослеживается правосторонний вывод (рис. 4.5) Здесь ко входной цепочке, так же как и при анализе LL(1)-грамматик, приписан концевой маркер $.

Рис. 4.5.
Основой цепочки называется подцепочка сентенциальной формы, которая может быть сопоставлена правой части некоторого правила вывода, свертка по которому к левой части правила соответствует одному шагу в обращении правостороннего вывода. Самая левая подцепочка, которая сопоставляется правой части некоторого правила вывода A


Формально, основа правой сентенциальной формы z - это правило вывода A





Вообще говоря, грамматика может быть неоднозначной, поэтому не единственным может быть правосторонний вывод




Чтобы восстановить этот вывод в обратном порядке, выделяем основу ?n в



в


Таким образом, главная задача анализатора типа сдвиг- свертка - это выделение и отсечение основы.
Преобразования КС-грамматик
Рассмотрим ряд преобразований, позволяющих "улучшить" вид контекстно-свободной грамматики без изменения порождаемого ею языка.
Назовем символ




Назовем символ


Очевидно, что каждый недостижимый и/или несводимый символ является бесполезным, как и все правила, его содержащие.
При внимательном изучении вышеприведенных определений становится понятным, что а) целесообразно искать не непосредственно сами недостижимые (или несводимые) символы, а последовательно определять множество достижимых (или сводимых) символов, начиная с тех, которые по определению являются достижимыми (аксиома) и сводимыми (терминалы) - все остальные символы оказываются бесполезными, б) одновременное определение достижимых и сводимых символов невозможно, так как соответствующие процессы идут в противоположных направлениях (от корня к листьям и наоборот).
Алгоритм 4.1. Устранение недостижимых символов.
Вход. КС-грамматика G = (N, T, P, S).
Выход. КС-грамматика G' = (N', T', P', S) без недостижимых символов, такая, что L(G') = L(G).
Метод. Выполнить шаги 1-4:
(1) Положить V0 = {S} и i = 1,
(2) Положить Vi = {X | в P есть A



(3) Если Vi

(4) Положить N' = Vi


Алгоритм 4.2. Устранение несводимых символов.
Вход. КС-грамматика G = (N, T, P, S).
Выход. КС-грамматика G' = (N', T', P', S) без несводимых символов, такая, что L(G') = L(G).
Метод. Выполнить шаги 1-4:
(1) Положить N' = T и i = 1,
(2) Положить

(3) Если Ni

(4) Положить G1 = ((N



Чтобы устранить все бесполезные символы, необходимо применить к исходной грамматике сначала Алгоритм 4.2, а затем Алгоритм 4.1.
Пример. Все символы следующей грамматики
S

A

B

являются достижимыми. Поэтому нарушение предложенного порядка применения к ней алгоритмов приведет лишь к частичному решению задачи.
КС-грамматика без бесполезных символов называется приведенной. Легко видеть, что для любой КС-грамматики существует эквивалентная приведенная. В дальнейшем будем предполагать, что все рассматривамые грамматики - приведенные.
Рекурсивный спуск
Выше был рассмотрен один из вариантов таблично-управ- ляемого предсказывающего анализа, когда магазин явно использовался в процессе работы анализатора. Возможен иной вариант предсказывающего анализа, в котором каждому нетерминалу сопоставляется процедура (вообще говоря, рекурсивная), и магазин образуется неявно при вызовах таких процедур. Процедуры рекурсивного спуска могут быть записаны, как показано ниже.
В процедуре A для случая, когда имеется правило A



Следствия определения LL(k)- грамматики
Теорема 4.6. КС-грамматика G = (N, ?, P, S) является LL(k)-грамматикой тогда и только тогда, когда для двух различных правил A







Доказательство. Необходимость. Допустим, что ?, A,





(Заметим, что здесь мы использовали тот факт, что N не содержит бесполезных нетерминалов, как это предполагается для всех рассматриваемых грамматик.) Если |x| < k; то y = z = e. Так как ?

Достаточность. Допустим, что G не LL(k)-грамматика.
Тогда найдутся такие два вывода

что цепочки x и y совпадают в первых k позициях, но ?





Пример 4.8. Грамматика G, состоящая из двух правил S

aS | a, не будет LL(1)-грамматикой, так как
FIRST1(aS) = FIRST1(a) = a.
Интуитивно это можно объяснить так: видя при разборе цепочки, начинающейся символом a, только этот первый символ, мы не знаем, какое из правил S




Удаление левой рекурсии
Основная трудность при использовании предсказывающего анализа - это нахождение такой грамматики для входного языка, по которой можно построить таблицу анализа с однозначно определенными входами. Иногда с помощью некоторых простых преобразований грамматику, не являющуюся LL(1), можно привести к эквивалентной LL(1)-грамматике. Среди этих преобразований наиболее эффективными являются левая факторизация и удаление левой рекурсии. Здесь необходимо сделать два замечания. Во-первых, не всякая грамматика после этих преобразований становится LL(1), и, во-вторых, после таких преобразований получающаяся грамматика может стать менее понимаемой.
Непосредственную левую рекурсию, то есть рекурсию вида A


A




где никакая из строк ?i не начинается с A. Затем заменяем этот набор правил на

где A' - новый нетерминал. Из нетерминала A можно вывести те же цепочки, что и раньше, но теперь нет левой рекурсии. С помощью этой процедуры удаляются все непосредственные левые рекурсии, но не удаляется левая рекурсия, включающая два или более шага. Приведенный ниже алгоритм 4.8 позволяет удалить все левые рекурсии из грамматики.
Алгоритм 4.8. Удаление левой рекурсии.
Вход. КС-грамматика G без e-правил (вида A

Выход. КС-грамматика G' без левой рекурсии, эквивалентная G.
Метод. Выполнить шаги 1 и 2.
(1) Упорядочить нетерминалы грамматики G в произвольном порядке.
(2) Выполнить следующую процедуру:

После (i-1)-й итерации внешнего цикла на шаге 2 для любого правила вида Ak





Алгоритм 4.8 применим, если грамматика не имеет e- правил (правил вида A

Варианты LR-анализаторов
Часто построенные таблицы для LR(1)-анализатора оказываются довольно большими. Поэтому при практической реализации используются различные методы их сжатия. С другой стороны, часто оказывается, что при построении для языка синтаксического анализатора типа "сдвиг-свертка" достаточно более простых методов. Некоторые из этих методов базируются на основе LR(1)-анализаторов.
Одним из способов такого упрощения является LR(0)- анализ - частный случая LR-анализа, когда ни при построении таблиц, ни при анализе не учитывается аванцепочка.
Еще одним вариантом LR-анализа являются так называемые SLR(1)-анализаторы (Simple LR(1)). Они строятся следующим образом. Пусть C = {I0, I1, ... , In} - набор множеств допустимых LR(0)-ситуаций. Состояния анализатора соответствуют Ii. Функции действий и переходов анализатора определяются следующим образом.
Если








Распространенным вариантом LR(1)-анализа является также LALR(1)-анализ. Он основан на объединении (слиянии) некоторых таблиц. Назовем ядром множества LR(1)-ситуаций множество их первых компонент (то есть во множестве ситуаций не учитываются аванцепочки). Объединим все множества ситуаций с одинаковыми ядрами, а в качестве аванцепочек возьмем объединение аванцепочек. Функции Action и Goto строятся очевидным образом. Если функция Action таким образом построенного анализатора не имеет конфликтов, то он называется LALR(1)-анализатором (LookAhead LR(1)).Если грамматика является LR(1), то в таблицах LALR(1) анализатора могут появиться конфликты типы свертка-свертка (если одно из объединяемых состояний имело ситуации [A









Восстановление процесса анализа после синтаксических ошибок
Одним из простейших методов восстановления после ошибки при LR(1)-анализе является следующий. При синтаксической ошибке просматриваем магазин от верхушки, пока не найдем состояние s с переходом на выделенный нетерминал A. Затем сканируются входные символы, пока не будет найден такой, который допустим после A. В этом случае на верхушку магазина помещается состояние Goto[s, A] и разбор продолжается. Для нетерминала A может иметься несколько таких вариантов. Обычно A - это нетерминал, представляющий одну из основных конструкций языка, например оператор.
При более детальной проработке реакции на ошибки можно в каждой пустой клетке анализатора поставить обращение к своей подпрограмме. Такая подпрограмма может вставлять или удалять входные символы или символы магазина, менять порядок входных символов.
В приведенных программах рекурсивного спуска была использована процедура реакции на синтаксические ошибки error(). В простейшем случае эта процедура выдает диагностику и завершает работу анализатора. Но можно попытаться некоторым разумным образом продолжить работу. Для разбора сверху вниз можно предложить следующий простой алгоритм.
Если в момент обнаружения ошибки на верхушке магазина оказался нетерминальный символ A и для него нет правила, соответствующего входному символу, то сканируем вход до тех пор, пока не встретим символ либо из FIRST(A), либо из FOLLOW(A). В первом случае разворачиваем A по соответствующему правилу, во втором - удаляем A из магазина.
Если на верхушке магазина терминальный символ, то можно удалить все терминальные символы с верхушки магазина вплоть до первого (сверху) нетерминального символа и продолжать так, как это было описано выше.
Атрибутные грамматики
Среди всех формальных методов описания языков программирования атрибутные грамматики (введенные Кнутом [7]) получили, по-видимому, наибольшую известность и распространение. Причиной этого является то, что формализм атрибутных грамматик основывается на дереве разбора программы в КС-грамматике, что сближает его с хорошо разработанной теорией и практикой построения трансляторов.
Язык описания атрибутных грамматик
Формализм атрибутных грамматик оказался очень удобным средством для описания семантики языков программирования. Вместе с тем выяснилось, что реализация вычислителей для атрибутных грамматик общего вида сталкивается с большими трудностями. В связи с этим было сделано множество попыток рассматривать те или иные классы атрибутных грамматик, обладающих "хорошими" свойствами. К числу таких свойств относятся прежде всего простота алгоритма проверки атрибутной грамматики на зацикленность и простота алгоритма вычисления атрибутов для атрибутных грамматик данного класса.
Атрибутные грамматики использовались для описания семантики языков программирования и было создано несколько систем автоматизации разработки трансляторов, основанных на формализме атрибутных грамматик. Опыт их использования показал, что "чистый" атрибутный формализм может быть успешно применен для описания семантики языка, но его использование вызывает трудности при создании транслятора. Эти трудности связаны как с самим формализмом, так и с некоторыми технологическими проблемами. К трудностям первого рода можно отнести несоответствие чисто функциональной природы атрибутного вычислителя и связанной с ней неупорядоченностью процесса вычисления атрибутов (что в значительной степени является преимуществом этого формализма) и упорядоченностью элементов программы. Это несоответствие ведет к тому, что приходится идти на искусственные приемы для их сочетания. Технологические трудности связаны с эффективностью трансляторов, полученных с помощью атрибутных систем. Как правило, качество таких трансляторов довольно низко из-за больших расходов памяти, неэффективности искусственных приемов, о которых было сказано выше.
Учитывая это, мы будем вести дальнейшее изложение на языке, сочетающем особенности атрибутного формализма и обычного языка программирования, в котором предполагается наличие операторов, а значит, и возможность управления порядком исполнения операторов. Этот порядок может быть привязан к обходу атрибутированного дерева разбора сверху вниз слева направо.
Что касается грамматики входного языка, то мы не будем предполагать принадлежность ее определенному классу (например, LL(1) или LR(1)). Будем считать, что дерево разбора входной программы уже построено как результат синтаксического анализа и атрибутные вычисления осуществляются в результате обхода этого дерева. Таким образом, входная грамматика атрибутного вычислителя может быть даже неоднозначной, что не влияет на процесс атрибутных вычислений.
При записи синтаксиса мы будем использовать расширенную БНФ. Элемент правой части синтаксического правила, заключенный в скобки [ ], может отсутствовать. Элемент правой части синтаксического правила, заключенный в скобки ( ), означает возможность повторения один или более раз. Элемент правой части синтаксического правила, заключенный в скобки [()], означает возможность повторения ноль или более раз. В скобках [ ] или [()] может указываться разделитель конструкций.
Ниже дан синтаксис языка описания атрибутных грамматик. Приведен только синтаксис конструкций, собственно описывающих атрибутные вычисления. Синтаксис обычных выражений и операторов не приводится - он основывается на Си.
Атрибутная грамматика::='ALPHABET' ( ОписаниеНетерминала ) ( Правило ) ОписаниеНетерминала::=ИмяНетерминала '::' [( ОписаниеАтрибутов / ';')]'.' ОписаниеАтрибутов::=Тип ( ИмяАтрибута / ',') Правило::='RULE' Синтаксис 'SEMANTICS' Семантика'.' Синтаксис::=ИмяНетерминала '::=' ПраваяЧасть ПраваяЧасть::=[( ЭлементПравойЧасти )] ЭлементПравойЧасти::=ИмяНетерминала | Терминал | '(' Нетерминал [ '/' Терминал ] ')' | '[' Нетерминал ']' | '[(' Нетерминал [ '/' Терминал ] ')]' Семантика::=[(ЛокальноеОбъявление / ';')] [( СемантическоеДействие / ';')] СемантическоеДействие::=Присваивание | [ Метка ] Оператор Присваивание::=Переменная ':=' Выражение Переменная::=ЛокальнаяПеременная | Атрибут Атрибут::=ЛокальныйАтрибут | ГлобальныйАтрибут ЛокальныйАтрибут::=ИмяАтрибута '<' Номер '>' ГлобальныйАтрибут::=ИмяАтрибута '<' Нетерминал '>' Метка::=Целое ':' | Целое 'Е' ':' | Целое 'А' ':' Оператор::=Условный | ОператорПроцедуры | ЦиклПоМножеству | ПростойЦикл | ЦиклСУсловиемОкончания
Описание атрибутной грамматики состоит из раздела описания атрибутов и раздела правил. Раздел описания атрибутов определяет состав атрибутов для каждого символа грамматики и тип каждого атрибута. Правила состоят из синтаксической и семантической части. В синтаксической части используется расширенная БНФ. Семантическая часть правила состоит из локальных объявлений и семантических действий. В качестве семантических действий допускаются как атрибутные присваивания, так и составные операторы.
Метка в семантической части правила привязывает выполнение оператора к обходу дерева разбора сверху- вниз слева направо. Конструкция i : оператор означает, что оператор должен быть выполнен сразу после обхода i- й компоненты правой части. Конструкция i E : оператор означает, что оператор должен быть выполнен, только если порождение i-й компоненты правой части пусто. Конструкция i A : оператор означает, что оператор должен быть выполнен после разбора каждого повторения i-й компоненты правой части (имеется в виду конструкция повторения).
Каждое правило может иметь локальные определения (типов и переменных). В формулах используются как атрибуты символов данного правила (локальные атрибуты) и в этом случае соответствующие символы указываются номерами в правиле (0 - для символа левой части, 1 - для первого символа правой части, 2 - для второго символа правой части и т.д.), так и атрибуты символов предков левой части правила (глобальные атрибуты). В этом случае соответствующий символ указывается именем нетерминала. Таким образом, на дереве образуются области видимости атрибутов: атрибут символа имеет область видимости, состоящую из правила, в которое символ входит в правую часть, плюс все поддерево, корнем которого является символ, за исключением поддеревьев - потомков того же символа в этом поддереве.
Значение терминального символа доступно через атрибут VAL соответствующего типа.
Пример 5.9. Атрибутная грамматика из примера 5.5
записывается следующим образом:
ALPHABET Num :: float V.Int :: float V; int P. Frac :: float V; int P. digit :: int VAL.
RULE Num ::= Int '.' Frac SEMANTICS V<0>=V<1>+V<3>; P<3>=1.
RULE Int ::= e SEMANTICS V<0>=0; P<0>=0.
RULE Int ::= digit Int SEMANTICS V<0>=VAL<1>*10**P<2>+V<2>; P<0>=P<2>+1.
RULE Frac ::= e SEMANTICS V<0>=0.
RULE Frac ::= digit Frac SEMANTICS V<0>=VAL<1>*10**(-P<0>)+V<2>; P<2>=P<0>+1.
Элементы теории перевода
До сих пор мы рассматривали процесс синтаксического анализа только как процесс анализа допустимости входной цепочки. Однако, в компиляторе синтаксический анализ служит основой еще одного важного шага - построения дерева синтаксического анализа. В примерах 4.3 и 4.8 предыдущей главы в процессе синтаксического анализа в качестве выхода выдавалась последовательность примененных правил, на основе которой и может быть построено дерево. Построение дерева синтаксического анализа является простейшим частным случаем перевода - процесса преобразования некоторой входной цепочки в некоторую выходную.
Определение. Пусть T - входной алфавит, а




Мы рассмотрим несколько формализмов для определения переводов: преобразователи с магазинной памятью, схемы синтаксически управляемого перевода и атрибутные грамматики
Классы атрибутных грамматик и их реализация
В общем виде реализация вычислителей для атрибутных грамматик вызывает значительные трудности. Это связано с тем, что множество значений атрибутов, связанных с данным деревом, приходится вычислять в соответствии с зависимостями атрибутов, которые образуют ориентированный ациклический граф. На практике стараются осуществлять процесс вычисления атрибутов, привязывая его к тому или иному способу обхода дерева. Рассматривают многовизитные, многопроходные и другие атрибутные вычислители. Это, как правило, ведет к ограничению допустимых зависимостей между атрибутами, поддерживаемых вычислителем.
Простейшими подклассами атрибутных грамматик, вычисления всех атрибутов для которых может быть осуществлено одновременно с синтаксическим анализом, являются S-атрибутные и L-атрибутные грамматики. Определение. Атрибутная грамматика называется S- атрибутной, если она содержит только синтезируемые атрибуты.
Нетрудно видеть, что для S-атрибутной грамматики на любом дереве разбора все атрибуты могут быть вычислены за один обход дерева снизу вверх. Таким образом, вычисление атрибутов можно делать параллельно с восходящим синтаксическим анализом, например, LR(1)- анализом.
Пример 5.8. Рассмотрим S-атрибутную грамматику для перевода арифметических выражений в ПОЛИЗ. Здесь атрибут v имеет строковый тип, k - обозначает операцию конкатенации. Правила вывода и семантические правила определяются следующим образом

Определение. Атрибутная грамматика называется L- атрибутной, если любой наследуемый атрибут любого символа Xj из правой части каждого правила X0

атрибутов символов X1, X2, . . . , Xj-1, находящихся в правиле слева от Xj , инаследуемых атрибутов символа X0.
Заметим, что каждая S-атрибутная грамматика является L-атрибутной. Все атрибуты на любом дереве для L- атрибутной грамматики могут быть вычислены за один обход дерева сверху-вниз слева-направо. Таким образом, вычисление атрибутов можно осуществлять параллельно с нисходящим синтаксическим анализом, например, LL(1)- анализом или рекурсивным спуском.
В случае рекурсивного спуска в каждой функции, соответствующей нетерминалу, надо определить формальные параметры, передаваемые по значению, для наследуемых атрибутов, и формальные параметры, передаваемые по ссылке, для синтезируемых атрибутов. В качестве примера рассмотрим реализацию атрибутной грамматики из примера 5.5 (нетрудно видеть, что грамматика является L-атрибутной).
void int_part(float * V0, int * P0) {if (Map[InSym]==Digit) { int I=InSym; float V2; int P2; InSym=getInSym(); int_part(&V2,&P2); *V0=I*exp(P2*ln(10))+V2; *P0=P2+1; } else {*V0=0; *P0=0; } } void fract_part(float * V0, int P0) {if (Map[InSym]==Digit) { int I=InSym; float V2; int P2=P0+1; InSym=getInSym(); fract_part(&V2,P2); *V0=I*exp(-P0*ln(10))+V2; } else {*V0=0; } } void number() { float V1,V3,V0; int P; int_part(&V1,&P); if (InSym!='.') error(); fract_part(&V3,1); V0=V1+V3; }
Обобщенные схемы синтаксически управляемого перевода
Расширим определение СУ-схемы, с тем чтобы выполнять более широкий класс переводов. Во-первых, позволим иметь в каждой вершине дерева разбора несколько переводов. Как и в обычной СУ-схеме, каждый перевод зависит от прямых потомков соответствующей вершины дерева. Во- вторых, позволим элементам перевода быть произвольными цепочками выходных символов и символов, представляющих переводы в потомках. Таким образом, символы перевода могут повторяться или вообще отсутствовать.
Определение. Обобщенной схемой синтаксически управляемого перевода (или трансляции, сокращенно: OСУ-схемой) называется шестерка Tr = (N,T,?,?,R,S), где все символы имеют тот же смысл, что и для СУ-схемы, за исключением того, что
?- конечное множество символов перевода вида Ai, где






A

Выход ОСУ-схемы определим снизу вверх. С каждой внутренней вершиной n дерева разбора (во входной грамматике), помеченной A, свяжем одну цепочку для каждого Ai. Эта цепочка называется значением (или переводом) символа Ai в вершине n. Каждое значение вычисляется подстановкой значений символов перевода данного элемента перевода Ai = vi, определенных в прямых потомках вершины n.
Переводом ?(Tr), определяемым ОСУ-схемой Tr, назовем множество {(x, y) | x имеет дерево разбора во входной грамматике для Tr и y - значение выделенного символа перевода Sk в корне этого дерева}.
Пример 5.4. Рассмотрим формальное дифференцирование выражений, включающих константы 0 и 1, переменную x, функции sin и cos , а также операции * и +.
Такие выражения порождает грамматика
E

T

F

Свяжем с каждым из E, T и F два перевода, обозначенных индексом 1 и 2. Индекс 1 указывает на то, что выражение не дифференцировано, 2 - что выражение продифференцировано. Формальная производная - это E2. Законы дифференцирования таковы:
d(f(x) + g(x)) = df(x) + dg(x) d(f(x) * g(x)) = f(x) * dg(x) + g(x) * df(x) d sin (f(x)) = cos (f(x)) * df(x) d cos (f(x)) = -sin (f(x))df(x) dx = 1 d0 = 0 d1 = 0
Эти законы можно реализовать следующей ОСУ-схемой:
E








Рис. 5.1.
F



Дерево вывода для sin (cos (x)) + x приведено на рис. 5.1.
Определение атрибутных грамматик
Атрибутной грамматикой называется четверка AG = (G, AS, AI, R), где
G = (N, T, P, S) - приведенная КС-грамматика;AS - конечное множество синтезируемых атрибутов;AI - конечное множество наследуемых атрибутов, AS


Атрибутная грамматика AG сопоставляет каждому символу X из N


Пусть правило p из P имеет вид X0

a(Xi) = f(b(Xj), c(Xk), ... , d(Xm))
где 0






Таким образом, семантическое правило определяет значение атрибута a символа Xi на основе значений атрибутов b, c, . . . , d символов Xj , Xk, . . . , Xm соответственно.
В частном случае длина n правой части правила может быть равна нулю, тогда будем говорить, что атрибут a символа Xi "получает в качестве значения константу".
В дальнейшем будем считать, что атрибутная грамматика не содержит семантических правил для вычисления атрибутов терминальных символов. Предполагается, что атрибуты терминальных символов - либо предопределенные константы, либо доступны как результат работы лексического анализатора.
Пример 5.5. Рассмотрим атрибутную грамматику, позволяющую вычислить значение вещественного числа, представленного в десятичной записи. Здесь N = {Num, Int, Frac}, T = {digit, .}, S = Num, а правила вывода и семантические правила определяются следующим образом (верхние индексы используются для ссылки на разные вхождения одного и того же нетерминала):

Для этой грамматики

Пусть дана атрибутная грамматика AG и цепочка, принадлежащая языку, определяемому соответствующей G = (N, T, P, S). Сопоставим этой цепочке "значение "следующим образом. Построим дерево разбора T этой цепочки в грамматике G. Каждый внутренний узел этого дерева помечается нетерминалом X0, соответствующим применению p-го правила грамматики; таким образом, у этого узла будет n непосредственных потомков (рис. 5.2).

Рис. 5.2.
Пусть теперь X - метка некоторого узла дерева и пусть a - атрибут символа X. Если a - синтезируемый атрибут, то X = X0 для некоторого




a(Xi) = f(b(Xj), c(Xk), ... , d(Xm))
все атрибуты b, c, . . . , d уже определены и имеют в узлах с метками Xj , Xk, . . . , Xm значения vj , vk, . . . , vm соответственно, а v = f(v1, v2, ... , vm). Процесс вычисления атрибутов на дереве продолжается до тех пор, пока нельзя будет вычислить больше ни одного атрибута. Вычисленные в результате атрибуты корня дерева представляют собой "значение", соответствующее данному дереву вывода.
Заметим, что значение синтезируемого атрибута символа в узле синтаксического дерева вычисляется по атрибутам символов в потомках этого узла; значение наследуемого атрибута вычисляется по атрибутам "родителя" и "соседей".
Атрибуты, сопоставленные вхождениям символов в дерево разбора, будем называть вхождениями атрибутов в дерево разбора, а дерево с сопоставленными каждой вершине атрибутами - атрибутированным деревом разбора.
Пример 5.6. Атрибутированное дерево для грамматики из предыдущего примера и цепочки w = 12:34 показано на рис. 5.3.

Рис. 5.3.
Будем говорить, что семантические правила заданы корректно, если они позволяют вычислить все атрибуты произвольного узла в любом дереве вывода.
Между вхождениями атрибутов в дерево разбора существуют зависимости, определяемые семантическими правилами, соответствующими примененным синтаксическим правилам. Эти зависимости могут быть представлены в виде ориентированного графа следующим образом.
Пусть T - дерево разбора. Сопоставим этому дереву ориентированный граф D(T), узлами которого являются пары (n; a), где n - узел дерева T, a - атрибут символа, служащего меткой узла n. Граф содержит дугу из (n1, a1) в (n2, a2) тогда и только тогда, когда семантическое правило, вычисляющее атрибут a2, непосредственно использует значение атрибута a1. Таким образом, узлами графа D(T) являются атрибуты, которые нужно вычислить, а дуги определяют зависимости, подразумевающие, какие атрибуты вычисляются раньше, а какие позже.
Пример 5.7. Граф зависимостей атрибутов для дерева разбора из предыдущего примера показан на рис. 5.4.

Рис. 5.4.
Можно показать, что семантические правила являются корректными тогда и только тогда, когда для любого дерева вывода T соответствующий граф D(T) не содержит циклов (то есть является ориентированным ациклическим графом).
Преобразователи с магазинной памятью
Рассмотрим важный класс абстрактных устройств, называемых преобразователями с магазинной памятью. Эти преобразователи получаются из автоматов с магазинной памятью, если к ним добавить выход и позволить на каждом шаге выдавать выходную цепочку.
Преобразователем с магазинной памятью (МП-преоб- разователем) называется восьмерка




Определим конфигурацию преобразователя P как четверку (q, x, u, y), где




Если множество D(q, a, Z) содержит элемент (r, u, z), то будем писать






Цепочку y назовем выходом для x, если





Будем говорить, что МП-преобразователь P является детерминированным (ДМП-преобразователем), если выполняются следующие условия:
для всех






Пример 5.1. Рассмотрим перевод ? , отображающий каждую цепочку

Этот перевод может быть реализован ДМП-преобразователем P = ({q0, qf}, {a, b, $}, {Z, a, b}, {a, b}, D, q0, Z, {qf}) c функцией переходов:

Схемы синтаксически управляемого перевода
Определение. Cхемой синтаксически управляемого перевода (или трансляции, сокращенно: СУ-схемой) называется пятерка Tr = (N, T, ?, R, S), где
(1) N - конечное множество нетерминальных символов;
(2) T - конечный входной алфавит;
? - конечный выходной алфавит;
R - конечное множество правил перевода вида

где

(5) S - начальный символ, выделенный нетерминал из N.
Определим выводимую пару в схеме Tr следующим образом:
(1) (S, S) - выводимая пара, в которой символы S соответствуют друг другу;
(2) если (xAy; x'Ay') - выводимая пара, в цепочках которой вхождения A соответствуют друг другу, и A





Переводом ? (Tr), определяемым СУ-схемой Tr, назовем множество пар

Если через P обозначить множество входных правил вывода всех правил перевода, то G = (N, T, P, S) будет входной грамматикой для Tr.
СУ-схема Tr = (N, T, ?, R, S) называется простой, если для каждого правила A

Перевод, определяемый простой СУ-схемой, называется простым синтаксически управляемым переводом (простым СУ-переводом).
Пример 5.2. Перевод арифметических выражений в ПОЛИЗ (польскую инверсную запись) можно осуществить простой СУ-схемой с правилами
E  | ET+ |
E  | T |
T  | TF+ |
T  | F |
F  | id |
F  | E. |
Найдем выход схемы для входа id * (id + id). Нетрудно видеть, что существует последовательность шагов вывода

переводящая эту цепочку в цепочку id id id + *.
Рассмотрим связь между переводами, определяемыми СУ- схемами и осуществляемыми МП-преобразователями [2].
Синтаксически управляемый перевод
Другим формализмом, используемым для определения переводов, является схема синтаксически управляемого перевода. Фактически, такая схема представляет собой КС- грамматику, в которой к каждому правилу добавлен элемент перевода. Всякий раз, когда правило участвует в выводе входной цепочки, с помощью элемента перевода вычисляется часть выходной цепочки, соответствующая части входной цепочки, порожденной этим правилом.
